Hall Effect
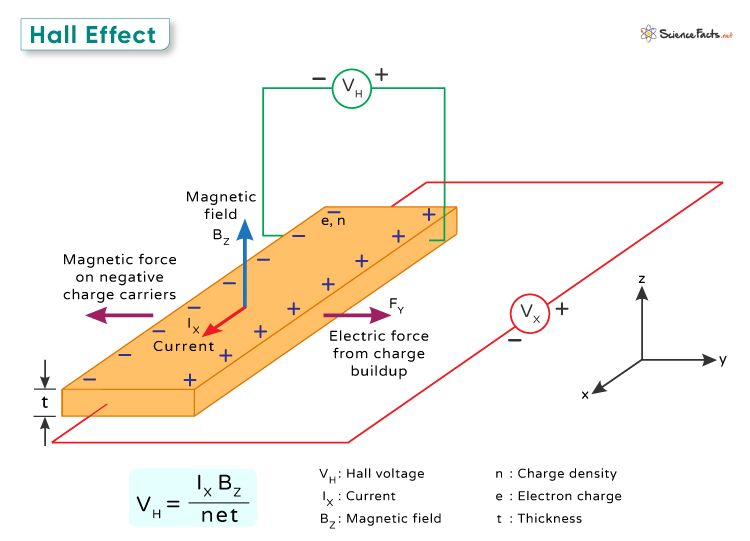
The Hall effect occurs when a magnetic field is applied at a right angle to an electric current flowing through a conductor. As a result, a voltage is created across the conductor, perpendicular to both the electric current and the magnetic field.
This phenomenon demonstrates how electric and magnetic fields can influence the movement of charged particles in a material. By studying the Hall effect, scientists can learn important information about the charge carriers, such as electrons, within the material.
This effect was discovered by American Physicist Edwin Hall in 1879.
Principle
When an electric current flows through a conductor, electrons move along its length in the opposite direction of the current. When a magnetic field is applied perpendicular to this current, something interesting happens. Each electron feels a force called the Lorentz force, which pushes it sideways, perpendicular to both the current direction and the magnetic field lines.
This sideways push is key to understanding the Hall Effect. Imagine electrons moving through a conductor because of an electric field that drives them forward. When a magnetic field is added, it exerts a sideways force on the electrons, making them move to one side of the conductor. As electrons gather on one side, they create a negative charge buildup, leaving a positive charge on the other side. This separation of charges creates an electric field inside the conductor that opposes further electron movement.
This process continues until the electric force from the charge buildup balances the magnetic force from the Lorentz force. The result is a stable situation where the forces are balanced, and a voltage, called the Hall voltage, is generated across the conductor.
Equation
In the previous section, we saw how Hall voltage is generated. The following expression gives its value:
Where
- VH is the Hall voltage
- Ix is the current flowing through the conductor
- Bz is the applied magnetic field
- n is the number of charge carriers per unit volume
- e is the value of the electric charge
- t is the thickness of the conductor
Hall Coefficient
The Hall coefficient is a fundamental parameter in understanding the behavior of charge carriers in materials subjected to a magnetic field. It is defined as the ratio of the Hall voltage to the product of the applied magnetic field, current density, and sample thickness. Mathematically, the Hall coefficient is given by
Where
- RH is the Hall coefficient
- Ey is the electric field due to the Hall effect
- jx is the current density
The Hall coefficient provides crucial insights into the material’s electronic properties. Its interpretation extends beyond a mere numerical value. It reflects the density and mobility of charge carriers within the material.
Applications
- Magnetic Field Sensing Equipment: Used to measure magnetic fields accurately in various applications, including scientific research and industrial processes.
- Current Sensors: Enables the measurement of electrical currents without direct contact, enhancing safety and reliability in electrical systems.
- Voltage Sensors: Utilized to measure voltages accurately across different systems, ensuring precise monitoring and control.
- Magneto-Resistive Sensors: Detects changes in magnetic fields by measuring resistance, commonly used in data storage devices, automotive applications, and more.
Aside, Hall effect can determine the carrier concentration, mobility, and conductivity of semiconductors.
Example Problems with Solutions
Problem 1: A thin rectangular metal plate of thickness 1 cm is subjected to a magnetic field of strength B = 0.5 T. When a current of I = 2 A flows through the plate, a Hall voltage of VH = 0.1 V is measured. Calculate the charge carrier density in the metal.
Solution
The Hall voltage can be calculated using the formula:
Rearranging the formula for n, we get:
Given data:
- Ix = 2 A
- Bz = 0.5 T
- VH = 0.1 V
- t = 1 cm = 0.01 m (converted to meters)
Substituting the values, we get:
The charge carrier density of the metal is 6.25 x 1021 m–3.
-
References
Article was last reviewed on Tuesday, June 10, 2025