Malus’ Law

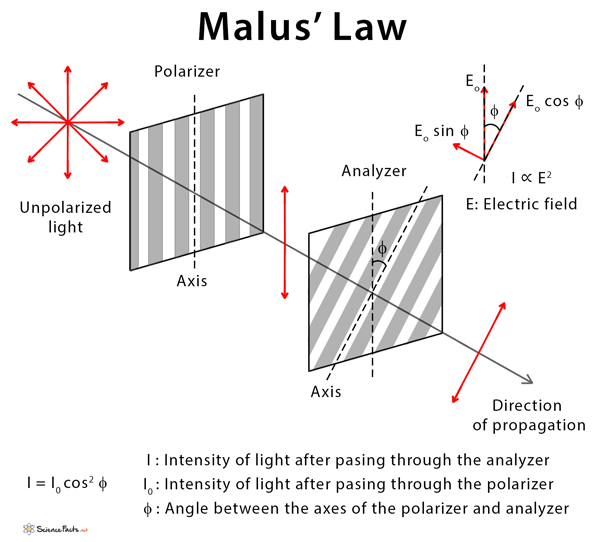
Light is an electromagnetic wave, which propagates as a transverse wave, with both the electric and magnetic fields oscillating perpendicularly to the direction of propagation. Natural light (e.g., sunlight) is unpolarized and vibrates in a multitude of directions. However, this light can be polarized by applying a filter, known as a polarizer. When a second filter is used in the path of the now polarized light, it is called an analyzer. Malus’ law states that the intensity of plane-polarized light passing through an analyzer varies as the square of the cosine of the angle between the transmission axes of the polarizer and analyzer.

Malus’ law has been named after Étienne-Louis Malus, who was a French engineer, physicist, and mathematician. Malus published his work on the polarization of light in 1809.

Consider a beam of light that is polarized after passing through the polarizer, and its electric field oscillates in one plane. The axis of the polarizer lies on this plane. Let this beam be incident on an analyzer whose axis makes an angle Ø with the axis of the polarizer. The component of the electric field E in the direction of the analyzer axis is given by,

E = E_o cos Ø

Where E_o is the amplitude of the electric field vector.

This equation gives the displacement of the electric field vector after passing through the analyzer. Since the intensity, I, of the polarized beam is proportional to the square of the electric field, therefore,

I ∝  E²

I = I_o cos² Ø

This equation is Malus’ law.

Note that,

When Ø = 0° ( or 180° ), I = I_o cos² 0° = I_o. This condition implies that the intensity of light transmitted by the analyzer is maximum when the transmission axes of the analyzer and the polarizer are parallel to each other.

When Ø = 90°, I = I_o cos² 90° = 0. This condition implies that the intensity of light transmitted by the analyzer is minimum when the transmission axes of the analyzer and the polarizer are perpendicular to each other.

Malus’s law is widely used in making polaroids that are used to control the intensity of light, as in sunglasses, window panes, and sometimes photographic and 3d movie cameras.