Toroid Magnetic Field
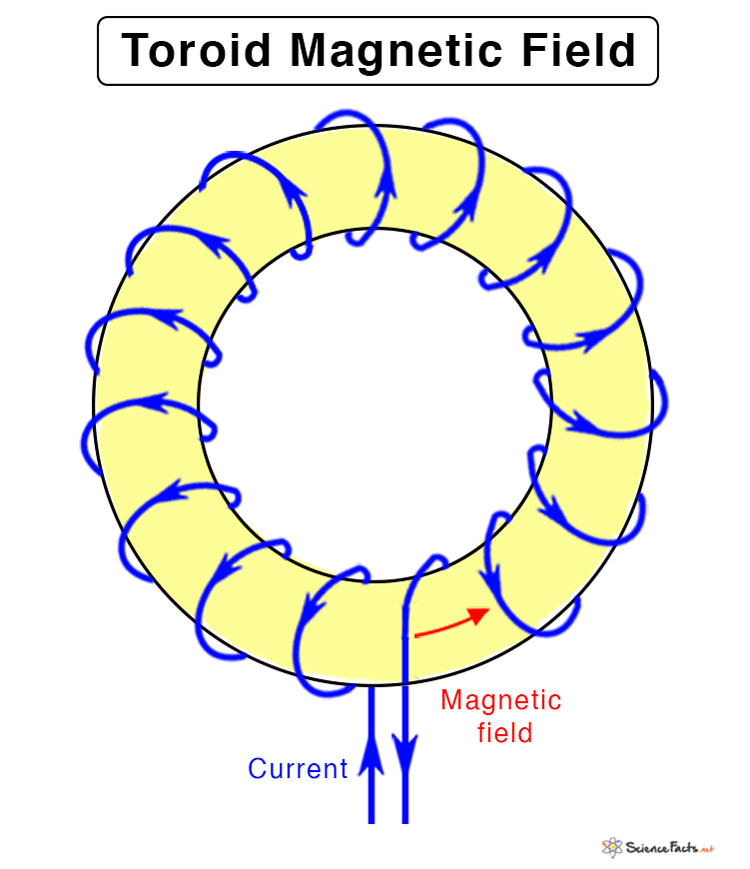
A toroid is an electromagnetic device consisting of a conducting wire wound into a coil around a metallic core bent into the shape of a circle. It is similar to a solenoid except that it is bent. Like any other electromagnetic device, a toroid produces a magnetic field when current is sent through the wire.
Toroid Magnetic Field Equation
Applying Ampere’s Law to Derive the Equation
The magnetic field of a toroid can be determined by using Ampere’s law, which gives a relationship between current and magnetic field. Ampere’s law states that the magnetic field produced by an electric current is proportional to the current’s magnitude. Mathematically, the integral of the magnetic field over a closed loop is equal to the product of the permeability and the current enclosed by the loop. The following equation shows the integral form.
Where,
Magnetic Field Inside the Toroid
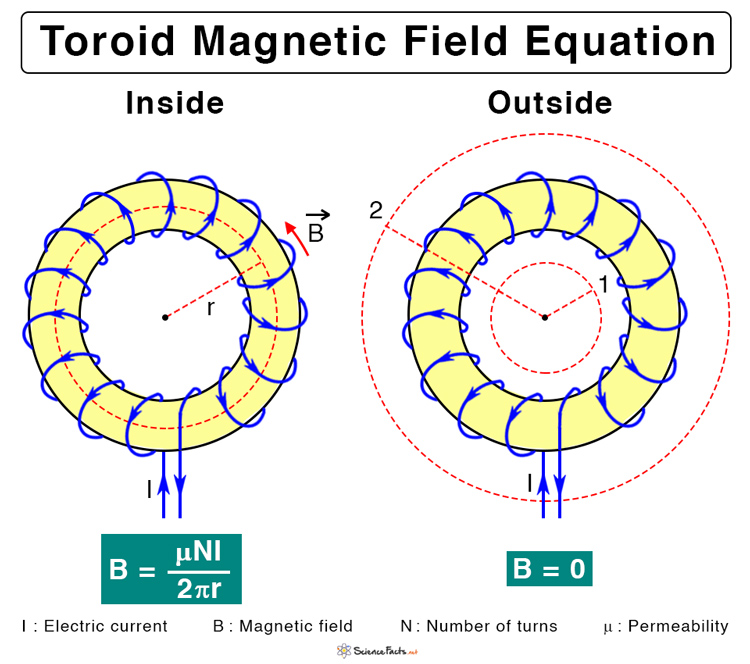
Consider a point at the center of the toroid (refer to the image below). Imagine a circle whose radius r is such that the circumference lies inside the toroid. If N is the number of turns and I is the current in each turn, then the current enclosed by the circle is given by, Ienc = NI.
Also, due to the symmetry of the toroid, B will be constant at every point in the circle. Further, the components of B perpendicular to the circle will cancel each other. Therefore, the tangential components are going to be non-zero.
Hence,
Integrating B around the loop gives the following:
Therefore, the magnetic field inside a toroid is not uniform and is inversely proportional to the distance from the center.
When the core is hollow, we replace the permeability of the medium with that of free space.
Where μo = permeability of air or vacuum (= 4π x 10-7 H/m)
Direction of Magnetic Field
Each loop in the toroid will give rise to a magnetic field in a direction given by the right-hand rule, and that direction is tangential to the circle. Hence, the direction of the magnetic field is tangential to the loop. This assumption was used during the derivation of the equation.
Magnetic Field Outside the Toroid
Imagine two concentric circles (circle 2 and circle 3 in the above image) outside the toroid. Circle 1 is smaller than the toroid, and circle 2 is bigger than the toroid. The current enclosed by circle 1 is zero since the loop does not pass through any conducting wire, or Ienc = 0. Hence, the magnetic field is zero, or B = 0.
Circle 2 encloses the entire coil that is wrapping the surface. The current passing through the surface in one direction exactly balances the current passing through the opposite direction. Therefore, there is no net current passing through the surface. Hence, Ienc = 0, and so B = 0.
For a point outside the toroid, the magnetic field is zero.
-
References
Article was last reviewed on Sunday, September 4, 2022