Archimedean Spiral
Definition: What is Archimedean Spiral?
If a line rotates in a plane about one of its ends and, at the same time, if a point moves along the line in one direction, then the curve traced out by the moving point is called a spiral. If the point is moving with a constant speed along the line that rotates with constant angular velocity, then the spiral traced by the point is called Archimedean Spiral. The point about which the line rotates is called a pole. Each complete revolution of the curve is termed the convolution.
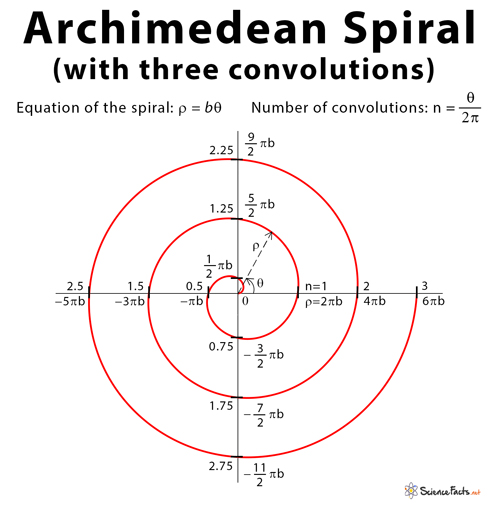
Equations of Archimedean Spiral
Arc Length of Archimedean Spiral
Applications of Archimedean Spiral
One of the applications of Archimedean Spiral is in the design of a spiral antenna. A spiral antenna operates over a wide range of radio frequencies. It is widely used in the defense industry for sensing applications and in the global positioning system (GPS).
Archimedean Spiral vs. Logarithmic Spiral
The logarithmic spiral can be distinguished from Archimedean spiral by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression. In contrast, in an Archimedean spiral, these distances are constant.
Article was last reviewed on Tuesday, January 21, 2020









