Gauss’s Law
What is Gauss’s Law
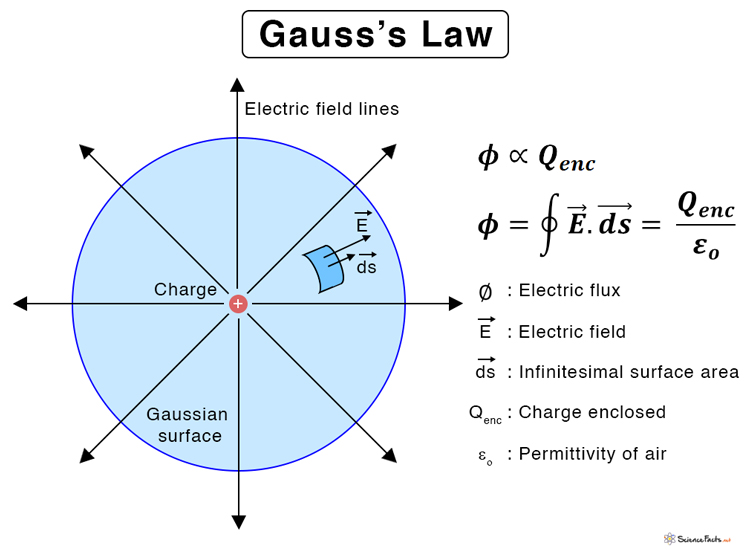
Gauss’s law is a general law in physics that gives a relationship between charges enclosed inside a closed surface to the total electric flux passing through the surface. The charges can be present in the air as point charges, inside a solid conductor, or on the surface of a hollow conductor.
What does Gauss’s Law State
According to Gauss’s law, the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
Gauss’s law has been named after German mathematician and physicist Karl Friedrich Gauss, who postulated it in 1867.
Conditions of Gauss’s Law
- The surface must be closed
- The surface must pass through the point where the electric field is calculated
- The charge must be inside the surface
- The charge distribution must be continuous. The law cannot be applied to discrete charges.
Gauss’s Law Equation
Mathematically, Gauss’s law states that the total flux within a closed surface is 1/ε0 times the charge enclosed by the closed surface.
Where,
φ: Electric Flux
Qenc: Charge enclosed
ε0: Permittivity of free space (= 8.85 x 10-12 C2N-1m-2)
SI unit for flux: Volt-meter or V-m
The Gauss’s law equation can be expressed in both differential and integral forms.
Problem 1: Find the flux through a spherical surface of radius a = 80 cm surrounding a charge of 12 nC.
Solution:
Given,
q = 12 nC = 12 x 10-9 C
The electric flux is given by,
Therefore,
φ = 12 x 10-9 C/8.85 x 10-12 N−1m−2 C2
or, φ = 1356 Nm2 C-1
Integral Form
The integral form of Gauss’s law can be expressed based on the definition of the electric flux. The electric flux in an area is defined as the electric field multiplied by the surface area projected in a plane perpendicular to the field. For a continuous surface, the flux can be evaluated by integrating the field over the surface.
Therefore,
Hence, Gauss’s law becomes
The above equation represents Gauss’s law in integral form using the SI unit. In the CGS unit, 1/ε0 = 4π. Then, the integral becomes,
Differential Form
The derivation of Gauss’s law in differential form uses the divergence theorem. The charge enclosed by the closed surface is the integral of the charge density over the surface volume.
Where,
ρ: Charge density
Therefore,
Here, we use the divergence theorem. The divergence theorem states that the surface integral of the electric field over a closed surface is equal to the volume integral of the divergence of the electric field over the surface.
Since the surface is arbitrary, if the integral is zero, the integrand is also zero.
Thus, the differential form of Gauss’s law states that the divergence of the electric field is equal to 1/ε0 times the density of charge enclosed by the closed surface.
Dielectric Medium
The above equations assume that the electric field is present in air or vacuum. In other words, there is no medium. Suppose there is a dielectric medium present in the region, then Gauss’s law modifies as follows.
Integral Form
Differential Form
Where,
k: Dielectric constant of the medium
Derivation of Gauss’s Law
Consider a point charge q in space. Coulomb’s law gives the electrical field E vector at a radial distance r.
Where
Now, imagine a closed surface such as a sphere of radius r that encloses the charge at its center.
An infinitesimal surface area on the sphere is given by
Therefore,
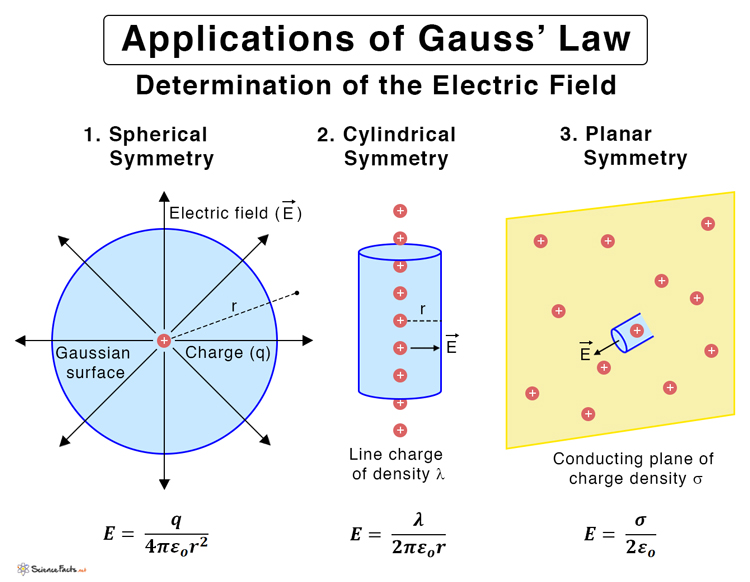
Importance and Applications of Gauss’s Law
The significance of Gauss’s law is that it can be used to solve complex electrostatic problems using symmetry. Gauss’s law is used to determine the electric field in many practical situations. Using a symmetric Gaussian surface to enclose the charges makes it easier to find the electric field. The reason is that symmetry cancels those components of the electric field that are equal and opposite. Thus, adding those components that are in the same direction gives the total electric field. Here are some examples where Gauss’s law can be applied.
1. Point Charge using Spherical Symmetry
Suppose a point charge +q rests in space. Consider a sphere of radius r that encloses the charge such that it lies at the center of the sphere. From the symmetry of the situation, it is evident that the electric field will be constant on the surface and directed radially outward.
Applying Gauss’ law, we get
The above equation gives the electric field magnitude at a distance r from a point charge +q. The result is similar to what one would obtain using Coulomb’s law. Hence, Gauss’s law can be applied to derive Coulomb’s law. In vector form, the electric field is given by
Problem 2: A point charge +2.2 pC is isolated in space. Find the electric field at a point 14 cm from the charge.
Solution:
Given,
q = 2.2 pC = 2.2 x 10-12 C
r = 14 cm = 0.14 m
The electric field equation is given by,
E = q/4πε0r2
Therefore,
E = 2.2 x 10-12 C/(4π x 8.85 x 10-12 N−1m−2 C2 x (0.14 m)2 )
Or, E = 1 N/C
2. Infinite Line Charge using Cylindrical Symmetry
Consider an infinite distribution of charge like a line charge with charge density λ. Imagine a cylindrical surface of radius r and height h that encloses the line charge, located at its axis. From the symmetry of the situation, it is clear that the electric field will be equal at every point on the surface and have a radial component only. Tangential components will cancel out. Therefore, the electric field is given by
An infinitesimal surface area on the cylinder is given by,
According to Gauss’s law,
The above equation represents the electric field at a distance r from an infinitesimally long line charge. In vector notation, the electric field is given by
Problem 3: An infinitely long line of charge carries 0.6 C along each meter of length. Find the electric field 3 cm from the line of charge.
Solution:
Given,
λ = 0.6 C/m
r = 3 cm = 0.03 m
The electric field equation is given by,
E = λ/2πε0r
Therefore,
E = 0.6 Cm-1/(2 x 3.14 x 8.85 x 10-12 N−1m−2 C2 x 0.03 m )
Or, E = 3.6 x 1011 N/C
3. Plane Charge using Planar Symmetry
Consider an infinite plane sheet with charge density σ. Now, consider a cylindrical surface that encloses the plane. The plane cuts the imaginary cylinder at its center. The symmetry of the situation dictates that the electric field must be perpendicular to the cross-section of the cylinder and the plane.
Therefore, for the top surface
And, for the bottom surface
Where
According to Gauss’s law,
The surface integral has several components.
Since the field is perpendicular to the curve surface, we have
The charge enclosed is given by
Therefore, from Gauss’ law
In vector notation,
Problem 4: A sizeable horizontal sheet of charge has a density of 5.0 × 10-6 C/m2. Calculate the electric field due to this charge distribution.
Solution:
Given,
σ = 5.0 × 10-6 C/m2
The electric field is given by,
E = σ/2ε0
Or, E = 5.0 × 10-6 Cm-2/(2 x 8.85 x 10-12 N−1m−2 C2)
Or, E = 2.82 x 105 C
-
References
Article was last reviewed on Sunday, September 4, 2022








very short and well analyzed notes that give more detail
Precise elaboration in an efficient manner.