Kepler’s Second Law
Kepler’s second law states “An imaginary line joining a planet and the Sun sweeps out equal areas in equal time intervals“.
Kepler’s second law describes the speed of a planet traveling in an elliptical orbit around the Sun. According to this law, the planet’s orbital radius and angular velocity will vary, but the angular momentum will be conserved. The planet’s speed increases as it approaches the Sun and decreases as it recedes. It is for this reason that Kepler’s second law is important. This law is also known as the Law of Equal Areas.
Equation
Suppose a planet sweeps out a small triangle with an altitude r and base r · dθ in an infinitesimal time dt, as shown in the image below.
Then, the area dA swept by the planet is
dA/dt represents the rate of change of velocity with time. Hence, it is the areal velocity. Therefore,
The angular momentum is given by
Therefore,
The rate of sweeping out an area on a planet’s orbit equals one-half the angular momentum divided by the mass. Since the only force present in the planet-Sun system is the radial gravitational force, angular momentum must be conserved. The term L/2m is a constant, so dA/dt is also a constant. Thus, Kepler’s second law arises due to the conservation of angular momentum.
-
References
Article was last reviewed on Thursday, June 16, 2022
Related articles
2 responses to “Kepler’s Second Law”
Leave a Reply
Join our Newsletter
Fill your E-mail Address
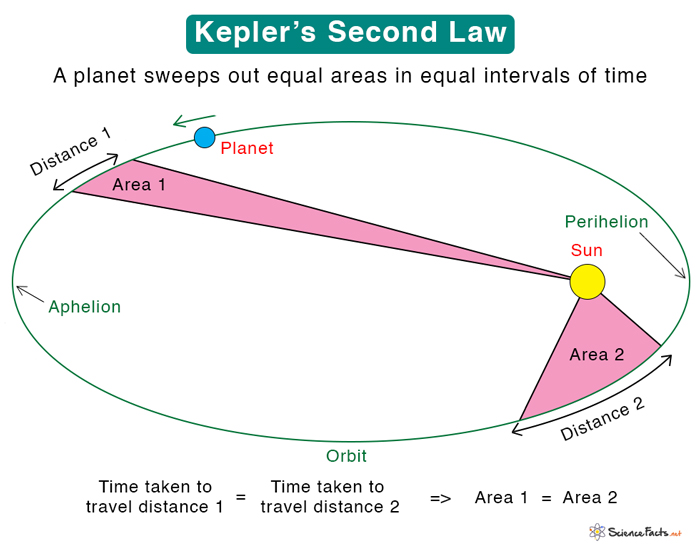
I assume that these graphics are schematic and not to scale? When I measure and use a triangle formula to check if the areas are in fact the same, one is almost double the area of the other.
You are right. They are not to scale.