Kirchhoff’s Law
Introduction: What is Kirchhoff’s Law?
Kirchhoff’s laws are a set of laws that quantify how current flows through a circuit and how voltage varies around a loop in a circuit. They are used to govern the conservation of charge and energy in standard electrical circuits. Two significant circuital laws are applied in every simple and complex electrical circuit in physics. These laws were postulated in 1845 by German physicist Gustav Kirchhoff. The proof of Kirchhoff’s law can be obtained by using Maxwell’s equations.
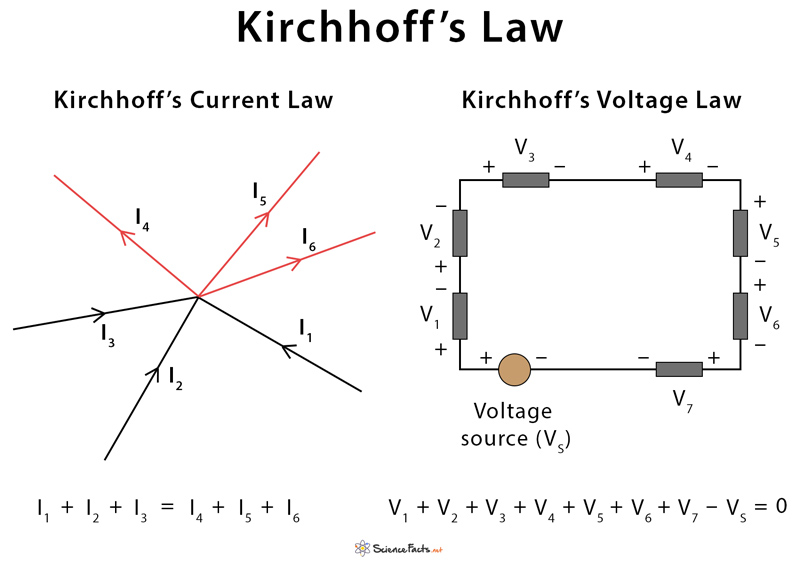
Kirchhoff’s Current Law (KCL) or Kirchhoff’s 1st Law
Current is defined as the rate of change of charge passing through a conducting wire. Kirchhoff’s current law states that the “total current entering a junction or node is exactly equal to the current leaving the node.” In other words, the algebraic sum of all the currents entering the node must be equal to the algebraic sum of all the currents leaving a node. This law is commonly known as the conservation of charge. The formula is given by
Σ Iin = Σ Iout
Kirchhoff’s Voltage Law (KVL) or Kirchhoff’s 2nd Law
Electric potential represents the concentration of energy in a circuit. The potential quickly spreads to a uniform value throughout an uninterrupted section of the electrical circuit. The difference in electric potential is called the voltage.
Kirchhoff’s voltage law states that “in any closed-loop network, the sum of voltage drops around the loop is equal to zero.” This law is known as the conservation of energy. The formula is given by
Σ Vtotal = 0
The term node in an electrical circuit generally refers to a connection or junction of two or more current-carrying paths. Also, for current to flow either in or out of a node, a closed-circuit path must exist.
Differences Between Kirchhoff’s Current and Voltage Laws
Kirchhoff’s Current Law vs. Kirchhoff’s Voltage Law | |
| KCL | KVL |
| States that the sum of all the currents entering a particular node is equal to the sum of all currents leaving the node | States that the sum of all the voltages around a closed path (loop) is zero |
| Nodal analysis is preferred to obtain node potentials as the currents entering/leaving the node can be expressed in terms of node potential | Loop analysis is preferred to obtain loop currents as loop potential differences can be expressed in terms of loop currents |
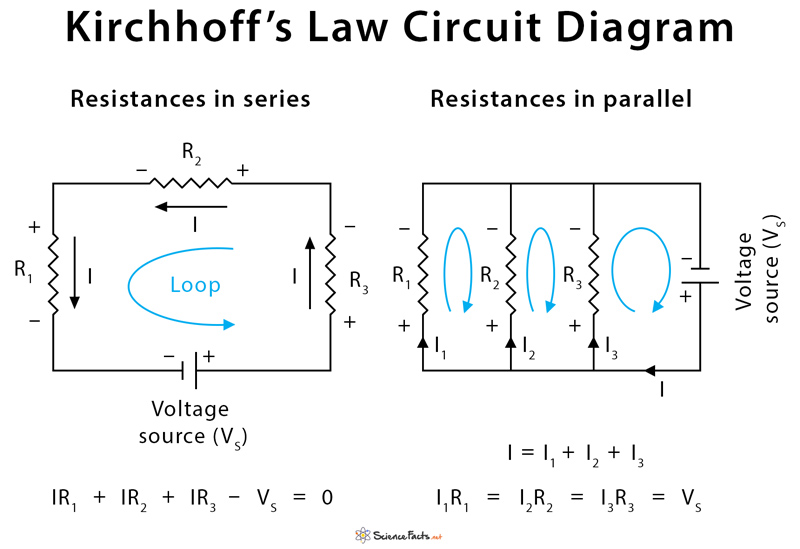
Kirchhoff’s Law Circuit Diagram
A circuit diagram consists of a source of current and voltage along with resistances and impedances, which can be in series, or parallel, or combination of the two. The polarity of the source is indicated by positive and negative signs, which automatically applies to the resistances.
Resistances in Series
Resistances are said to be in series when they are connected in a single path. The current from a source flows through all the resistances in a closed loop.
Resistances in Parallel
Resistances are said to be in parallel when the path branches and each branch consists of one resistance. The current from the source splits into different paths. The equation for replacing resistances in parallel is a bit more complicated.
Sign Convention
The sign convention for applying signs to the voltage polarities in KVL equations is as follows. When traversing the loop, if the positive terminal of a voltage difference is encountered before the negative terminal, the voltage difference will be interpreted as positive. If the negative terminal is encountered first, the voltage difference will be interpreted as negative.
Applications of Kirchhoff’s Law
Kirchhoff’s laws are applicable to analyze any circuit regardless of the composition and structure of it. Some of its applications include
- To find the unknown resistances, impedances, voltages, and currents (direction as well as value).
- In a branched circuit, currents passing each branch are determined by applying KCL at every junction and KVL in every loop.
- In a looped circuit, the current passing each independent loop is determined by applying KVL for each loop and calculating the currents in any resistance of the circuit.
Limitations of Kirchhoff’s Law
Kirchhoff’s laws are limited in their applicability. They are valid for all cases in which total electric charge is constant in the region into consideration. Essentially, this is always true, so long as the law is applied for a specific point. Over a region, however, charge density may not be constant. Because the charge is conserved, the only way this is possible is if there is a flow of charge across the boundary of the region. This flow would result in current, thus violating Kirchhoff’s laws.
Another limitation is that it works under the assumption that there is no fluctuating magnetic field in the closed-loop. Electric fields and emf could be induced, which causes Kirchhoff’s laws to break in the presence of a variable magnetic field.
-
References
Article was last reviewed on Friday, February 3, 2023








Satisfactory.