Newton’s Rings
Definition: What are Newton’s Rings?
Newton’s rings are a series of concentric circular rings consisting of bright- and dark-colored fringes. When a plano-convex lens lies on top of a plane lens or glass sheet, a small layer of air is formed between the two lenses. Newton’s rings are formed by the interference phenomenon when monochromatic and coherent rays of light are reflected from the top and bottom surfaces of this air film. The film’s thickness varies from zero at the point of contact to a finite value in the wedge-shaped region.
By studying the pattern of concentric rings, it is possible to determine the wavelength of monochromatic light and the refractive index of a given transparent liquid medium present in a wedge-shaped film. If white light is used instead of monochromatic, the lens system produces colorful interference, since the condition for a maximum in the interference is dependent on the wavelength.
Newton’s rings have been named after English physicist and mathematician Sir Isaac Newton, who was the first to observe the effect in 1704.
Principle of Newton’s Rings Formation
The phenomenon of the formation of Newton’s rings can be explained based on the wave theory of light.
- An air film of varying thickness is formed between the lens and the glass sheet.
- When a ray falls on the surface of the lens, it is reflected as well as refracted.
- When the refracted ray strikes the glass sheet, it undergoes a phase change of 180° on reflection.
- Interference occurs between two waves that interfere constructively if the path difference between them is (m+1/2)λ and destructively if the path difference between them is mλ, thereby producing alternate bright and dark rings.
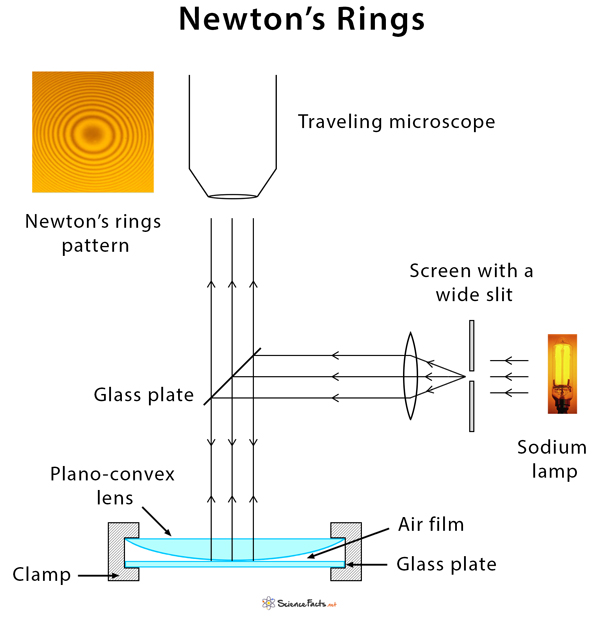
Newton’s Rings Experiment
Apparatus
The apparatus consists of the following components.
- Nearly monochromatic source of light (sodium light)
- Plano-convex lens
- Optically flat glass plates
- Convex lens
- Traveling microscope
Method
The experimental setup for Newton’s ring is shown in the figure above. The convex surface of a plano-convex lens having a long focal length (large radius of curvature) is placed in contact with a plane glass plate and clamped together. Light from a monochromatic source (e.g., sodium lamp) is allowed to fall on a convex lens through a wide slit, which renders it into a nearly parallel beam. At first, light falls on a glass plate inclined at an angle of 45° to the vertical before reaching the lens-plate system at the bottom. Light is reflected from the upper surface of the glass plate and the lower surface of the lens. Due to the air film formed by the glass plate and lens, interference fringes are formed, which are observed directly through a traveling microscope. The rings are concentric circles. A dark central spot is obtained when viewed by reflection.
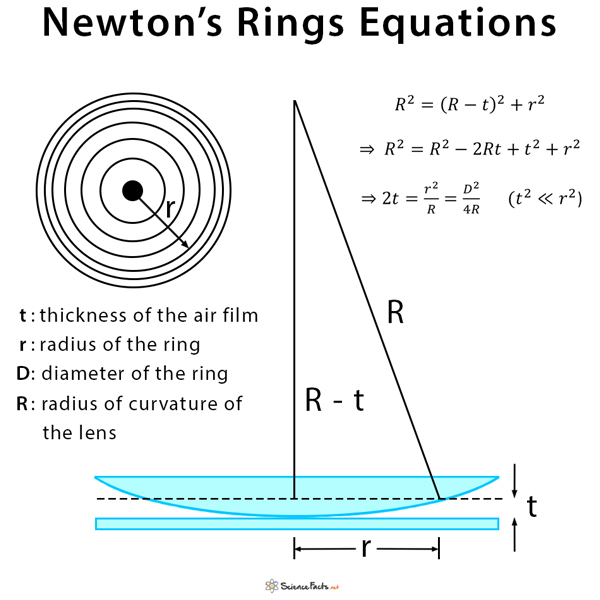
Theory and Equations
Consider a ray of light incident on the air film at a point where its thickness is t. The optical path difference between the two reflected rays will be 2t. Taking into account the phase change of 180° for reflection at the rare to the dense surface, the conditions for constructive and destructive interference are
2t = (m+1/2)λ (for constructive interference or bright rings)
2t = (m+1/2)λ (for destructive interference or dark rings)
where m is the order of the ring and can take the values m = 0, 1, 2, 3, …, n
If R is the radius of curvature of the lens and r is the distance of the point under consideration to the point of contact of the lens and glass plate, then
R2 = (R-t)2 + r2
or, R2 = R2 – 2Rt + t2 + r2
or, 2t = r2/R = D2/4R
since t2 << r2 and D = 2r, the diameter of a ring.
Combine this result with the condition for the mth and nth dark rings. Then, the diameters of the two rings are given by
Dm2 = 4Rmλ
Dn2 = 4Rnλ
Subtracting the two equations and rearranging
Dn2 – Dm2 = 4R(n-m)λ
λ = (Dn2 – Dm2)/4R(n-m)
Thus, the wavelength λ can be determined from this equation.
If a liquid of refractive index μ is introduced between the lens and the plate, then the path difference is given by 2μt. The diameter of any ring will be less with the liquid in place than without it. The equation for wavelength is given by
λ = (Dn2 – Dm2)μ/4R(n-m)
In a laboratory experiment, students are required to calculate the radius of curvature R of the lens. It is calculated by spherometer using the following relation
R = l2/6h + h/2
Here, l is the mean length of the three sides of the equilateral triangle formed by joining the tips of three outer legs, and h represents the height of the central screw above or below the plane of the outer legs.
Image courtesy: Softsolder.com
Newton’s Rings Video
Newton’s Rings in Transmitted Light
Newton’s rings are studied in transmitted light as well. The interference conditions for reflection and transmitted light are complementary. The diameters of the bright rings calculated for transmitted light using the equations above correspond precisely to the diameters of the dark rings in reflection. In particular, the center of Newton’s rings is bright in transmitted light and dark in reflection.
Applications of Newton’s Rings
Newton’s rings are a phenomenon that can be viewed daily. Some of its applications are as follows.
- For testing the uniformity of a polished surface by studying the interference pattern the surface makes when placed in contact with a perfectly flat glass surface
- To control the thickness of paint that is used on posters. Too much paint would exceed total weight requirements, and too little would result in faint imprints.
FAQs
Ans. The plano-convex lens is circular. All the bright and dark fringes are the loci of the points of the film of equal thickness. As the equally thick films are formed along the diameter of the circular shape, the fringe pattern is also circular.
Ans. At the point of contact of the lens with the glass plate, the thickness of the air film is minimal compared to the wavelength of light. Therefore, the path difference introduced between the interfering waves is zero, the condition of minimum intensity. Consequently, the interfering waves at the center are opposite in phase and interfere destructively.
Ans. Sodium light is used in Newton’s rings experiment because it is monochromatic, and the two spectral lines of sodium can be resolved without difficulty.
-
References
Article was last reviewed on Friday, February 3, 2023









The diagram may be mislabeled. Perhaps R and RT are the wrong way around.
Thank you for your comment. We have edited the image.
this content is very nice,very useful for me and thank u so much