Standing Waves
Definition: What is a Standing Wave?
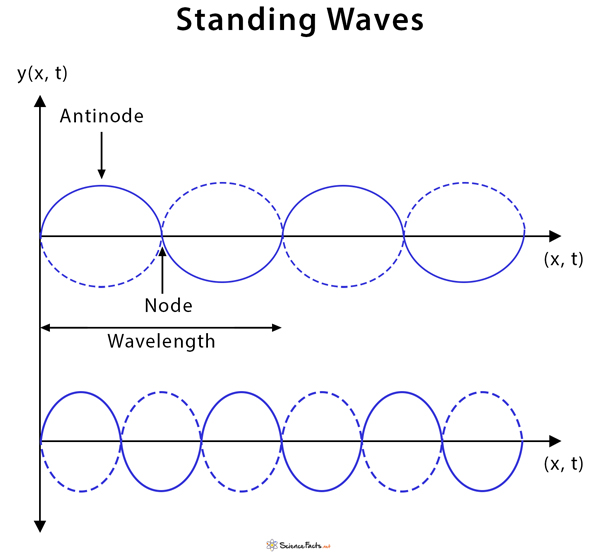
Standing wave, also called a stationary wave, is a combination of two waves moving in opposite directions, each having the same amplitude and frequency. This phenomenon is a result of interference of these two waves with their amplitudes either adding or canceling out. Because the observed wave pattern is characterized by points that appear to be standing still, the pattern is often called a standing wave pattern.
Standing Wave Animation
Image Courtesy: Physicsclassroom.com
Examples of Standing Waves
These are a few situations where standing waves can be observed.
- Two people shaking either end of a jump rope
- Ocean or pool waves hitting a wall and bouncing back in the opposite direction
- Plucking the strings of a guitar. A guitarist can purposely alter the pitch of the sound by placing a finger on the string to shorten the length that is vibrating.
- Wind instruments that have air columns in them. The effective length of the tube determines the sound the pipe makes.
- In plates, rods, and diaphragms that are parts of percussion instruments and form an essential feature in many musical instruments
- In optical media, such as optical cavities and waveguides.
How are Standing Waves Formed?
Standing waves can form under a variety of conditions. However, they are easily demonstrated in a medium that is finite or bounded. In general, standing waves can be produced by two identical waves traveling in opposite directions with the right wavelength. In a bounded medium, the vibrational waves emitted by a source are reflected from one end of the medium and interfere with the incident waves. The interference of these two waves produces a resultant wave that is stationary, i.e., a pattern that does not appear to move.
There is always energy associated with standing waves. This energy travels through a medium as a transverse pulse.
Terms Associated with Standing Waves
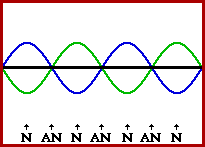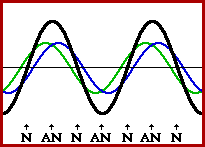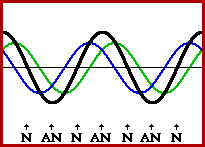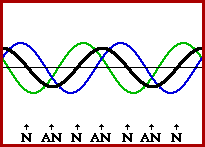
Nodes: Points on a standing wave where the wave stays in a fixed position over time because of destructive interference.
Antinodes: Points on a standing wave where the wave vibrates with maximum amplitude due to constructive interference.
Fundamental frequency: Lowest frequency of a standing wave that has the fewest number of nodes and antinodes.
Harmonics: Higher frequencies that are integral multiples of the fundamental frequency.
Standing Wave Equation
Consider two sine waves of the same angular frequency (ω), wavelength (λ), wavenumber (k), and amplitude (A) that move in opposite directions. The displacements (y) of the waves as a function of position (x) and time (t) are described by
y1 = (A/2) sin (kx – ωt)
y2 = (A/2) sin (kx + ωt)
where the first wave is moving toward the right (positive x), and the second wave is moving toward the left (negative x). The factor of 1/2 is placed for convenience. Adding these two waves gives the total displacement at any point and time:
yT = y1 + y2 = (A/2) sin (kx – ωt) + (A/2) sin (kx + ωt) = (A/2)[sin (kx – ωt) + sin (kx + ωt)]
Recall that,
Sin (A+B) = sin A cos B + cos A sinB
Sin (A-B) = sin A cos B – cos A sin B
Therefore,
Sin (A-B) + Sin (A+B) = 2 sin A cos B
Hence,
yT = (A/2) 2sin (kx) cos (ωt)
Or, yT = sin (kx) cos (ωt)
In the boldface equation above, the displacement varies with distance as sin kx, but changing the time does not shift the location of peaks and troughs. It merely changes the amplitude. For example, at x=0, the displacement is always zero, no matter what the value of t. Hence, the velocity of a standing wave is zero.
Standing Waves in a String
Standing waves are readily observed on a string, where the ends are fixed, and the string does not move. Places, where the string is not vibrating, are the nodes. The nodes limit the wavelengths that are possible, which in turn determines the possible frequencies since the speed of sound is fixed. The lowest frequency is called the fundamental frequency. Higher frequencies are all multiples of the fundamental frequency and are called harmonics. The various harmonics are also called the normal modes of vibration of the string.
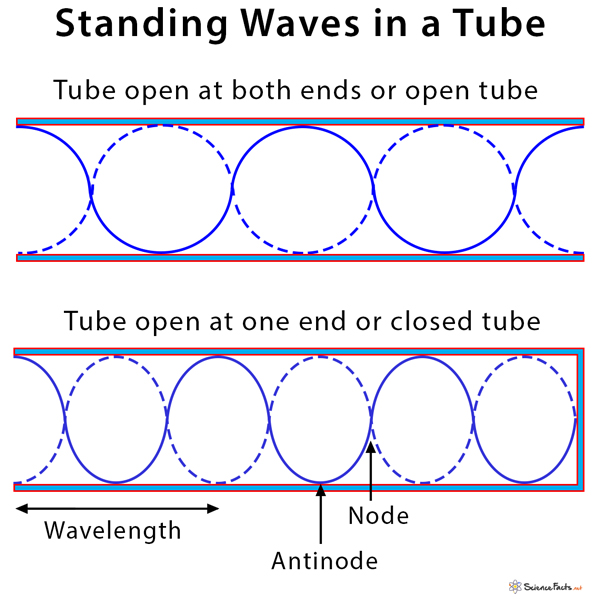
Standing Waves in Air Columns – Open and Closed Tube
Standing waves are a common phenomenon in air columns, pipes, and tubes. Waves are created at one end of the tube by something that vibrates. The waves then travel to the end of the tube and reflect. A standing wave is created by the waves traveling in each direction. Since the wave is traveling in the air, it will move at the speed of sound in air at the ambient temperature.
The length of a tube determines the frequency of a standing wave in the tube. Several complications arise depending on if one or both ends are closed or open. If an end is open, the air can move freely, and so there is maximum air movement or a displacement antinode at that end.
An open tube or pipe is defined as one that is open at both ends. For such a tube, a standing wave can form if the wavelength of sound results in antinodes at both ends.
Many musical instruments are made of a tube that is closed at one end but opened at the other. Such an instrument is known as a closed tube or pipe. Like an open tube, they can form a standing wave with the sound of an appropriate frequency. In this case, the resultant wave pattern forms an antinode at the open end and a node at the closed end.
Applications of Standing Wave
- Detect leakage in pipeline systems
- X-ray standing wave (XSW) method is applied for the investigation of the real structure of crystals
- For calibrating commercial and reference attenuators used in laboratories
-
References
Article was last reviewed on Friday, February 17, 2023