Torque
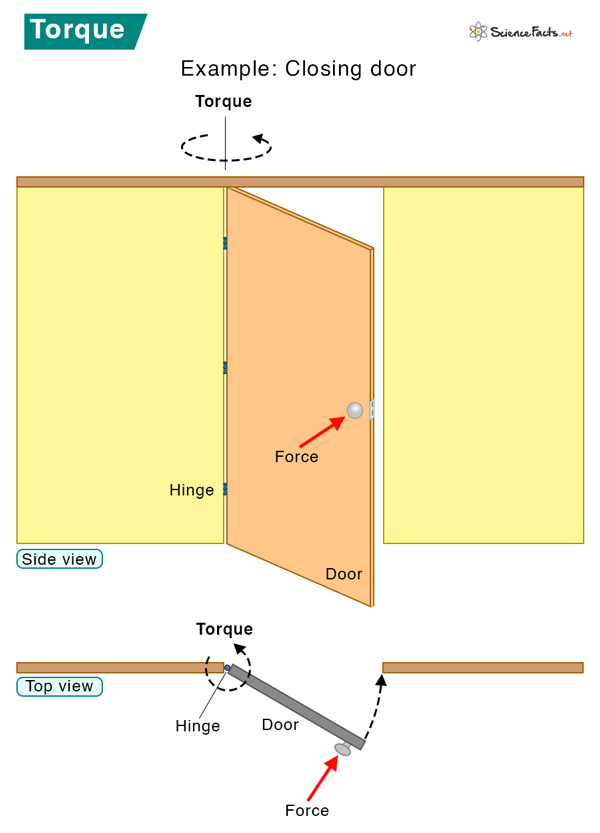
Torque represents the force that causes an object to rotate about an axis. Just as force causes an object to accelerate in a straight line, torque makes the object rotate about an axis with angular acceleration. Torque is a vector quantity whose direction depends on the force.
Types and Examples of Torque
Torque can be of two types – static and dynamic
A static torque does not produce angular acceleration. For example, pushing a closed door is a static torque. You are applying a force on the door, yet it does not rotate about its hinges (axis) because it is closed. Another example is pedaling a cycle at a constant speed.
A dynamic torque produces angular acceleration. For example, the drive shaft of a racing car produces angular acceleration allowing the race car to drive on its track. A wrench is activated by force applied at one end, creating an unbalanced torque on the tightened element.
Torque Formula
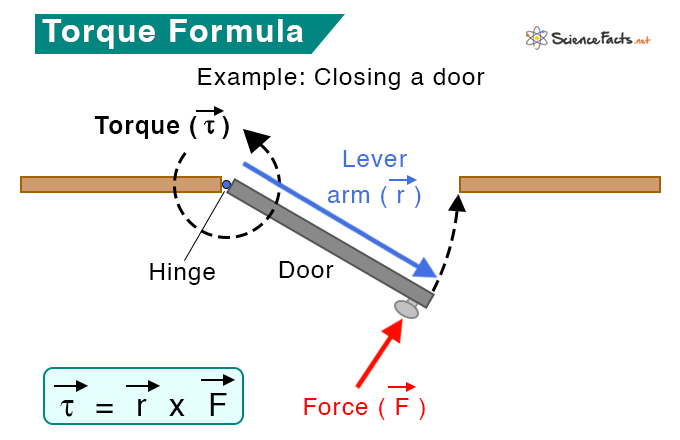
Torque is the product of force and distance of the point of application of force and the axis of rotation.
Because it is a product of some distance and a physical entity like force, torque is also called moment of force. r is called the length of the moment arm or lever arm. Also, since the rotating object describes a circle, r is the radius. Notice that the longer the lever arm, the higher the torque.
As mentioned before, torque is a vector quantity. Therefore, in vectorial notation, torque is given by
Using the right-hand rule, we can find the direction of the torque vector. If we put our fingers in the direction of
Suppose the angle between
Symbol & Unit
The Greek symbol τ represents torque. The unit of force is Newton, and that of distance is meter. Therefore, the unit of torque is Newtonˑmeter (Nm). The dimension of torque is ML2T-2.
From the above equation, when
The static torque can be easily measured by using the formula. The dynamic torque is challenging to measure. One can measure the bending force and torque using strain gauges at the pivot point.
Torque and Rotational Kinematics
Newton’s second law for rotational motion states that every object will move with a constant angular velocity unless a torque acts on it. According to the second law for rotation,
Where,
α: Angular acceleration
Therefore, the torque is directly proportional to the moment of inertia and angular acceleration. The above equation is an essential equation for studying rotational kinematics. Rearranging it, we find that
The greater the torque, the higher the angular acceleration. Also, for a massive object, the moment of inertia is high. Hence, the angular acceleration is low.
Rotational Equilibrium
An object can be subjected to several torques. If the net torque on the object is zero, it is in rotational equilibrium.
Suppose forces F1, F2, …, and Fn act at distances r1, r2, …, and rn from the pivot point or fulcrum. Then the torque balance equation is
Power
When an object rotates, there will be energy associated with it. We calculate the power of the object as follows.
Where ω is the angular velocity. The power is the product of the torque and the angular velocity.
Applications
Torque is applied to any object where there is a pivot point. Here are some applications.
- Wrench
- Seesaw
- Pendulum
- Steering wheel
Solved Problems
Problem 1. A 4 m beam of negligible weight balances in equilibrium with a fulcrum placed 1.5 m from its left end. If a force of 60 N is applied on its right end, how much force must be applied to the left?
Solution
Given F1 = ?, r1 = 1.5 m, F2 = 60 N, r2 = 4 m – 1.5 m = 2.5 m
Torque on the left lever arm (τ) = r1 x F1 = 1.5 m x F1
Torque on the right lever arm (τ) = r2 x F2 = 2.5 m x 60 N = 150 Nˑm
Since the beam is balanced, the two torques cancel out. Therefore,
τ1 = τ2
=> 1.5 m x F1 = 150 Nˑm
=> F1 = 150 Nˑm /1.5 m = 100 N
Problem 2. One side of a seesaw carries a 32 kg mass four meters from the fulcrum and a 36.5 kg mass two meters from the fulcrum. To balance the seesaw, what mass should be placed eight meters from the fulcrum on the side opposite the first two masses?
Solution
Given m1 = 32 kg, r1 = 4 m, m2 = 36.5 kg, r2 = 2 m, m3 = ?, r3 = 8 kg
Using the torque balance equation
r1ˑF1 + r2ˑF2 + r3ˑF3 = 0
=> 4 m ˑ 32 kg ˑ g + 2 m ˑ 36.5 kg ˑ g – 8 m ˑ m3 ˑ g = 0
m3 = (4 m ˑ 32 kg + 2 m ˑ 36.5 kg)/8 m = 25.1 kg
FAQs
Ans. Torque is a counterpart of force in rotational mechanics. The critical difference between the two is that torque is the capability of a force to produce a rotation around an axis.
Ans. Torque measures an engine’s capacity to do work, whereas horsepower measures how fast the engine can perform work.
-
References
Article was last reviewed on Friday, October 18, 2024