Wien’s Law

Wien’s law, also known as Wien’s displacement law, gives a relationship between the wavelength of thermal radiation and the temperature at which a blackbody emits the radiation. According to this law, the temperature is inversely proportional to the wavelength at which the radiation has maximum intensity.

This law is named after German physicist Wilhelm Wien who derived it in 1893.

Formula

Wien found that the radiative energy per second per wavelength interval \( \left( \frac{dW}{d\lambda } \right) \) has a maximum at a particular wavelength (λ_m). The maximum shifts to shorter wavelengths as the temperature (T) is increased. The shift of the maximum is a direct consequence of Planck’s radiation law, which establishes blackbody radiation intensity as a function of wavelength at any given temperature. Mathematically, the following equation represents Wien’s law:

Where

λ_max: Wavelength at which the radiation intensity is maximum, known as peak wavelength

b: A constant called Wien’s constant, whose value is 2.897 x 10^-3 m·K

T: Absolute temperature

The above equation can be written in a more generalized form.

λ_max x T = 2.897 x 10^-3 m·K

The radiation at peak wavelength that a blackbody emits makes it simple to estimate the approximate temperature of hot bodies. As this is an inverse relationship, the higher the temperature, the shorter the wavelength. It implies that hot objects emit radiation in the violet or ultraviolet end of the visible spectrum. On the other hand, the lower the temperature, the longer the wavelength. It means that cold objects emit radiation in the red or infrared end of the visible spectrum. This is why hotter objects appear blue and colder objects appear red.

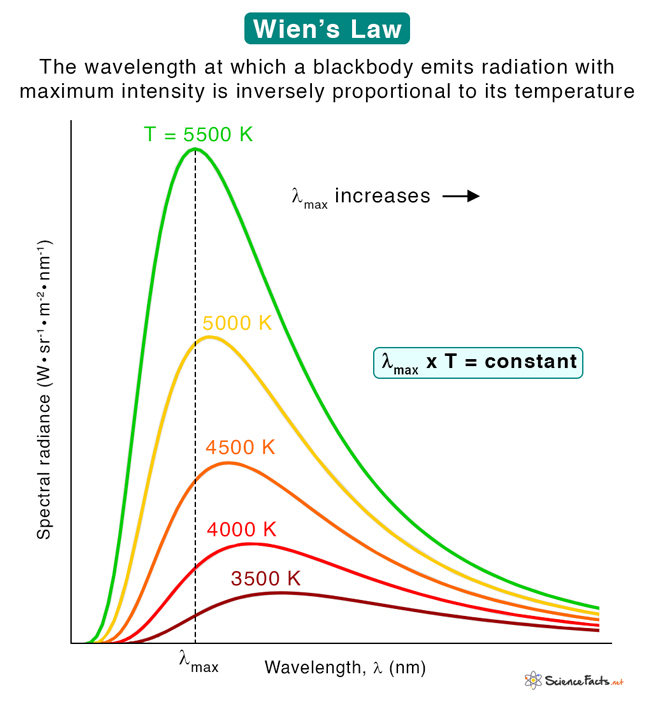
Wien’s Law Graph

The shift in the peak wavelength can be traced through a set of intensity vs. wavelength curves at different temperatures, as shown in the image below. These curves are known as Planck curves. Each curve passes through a maximum corresponding to the peak wavelength. The different values of λ_max and T satisfy Wien’s law equation.

Applications

• To study blackbody curves and determine the temperatures of stars, including the Sun
• To make LED light bulbs with different colors and temperatures – Warm white is between 2700 and 3200 K. Natural white is between 4000 and 4500 K. Cool white is between 7000 and 7500 K.

Solved Problems

Problem 1. The average surface temperature of the Sun is approximately 5778 K. What wavelength in nanometers is the peak intensity of the light coming from the Sun? What part of the visible spectrum does this wavelength correspond to?

Solution

Given T = 5778 K

Wien’s law equation is

λ_max x T = 2.897 x 10^-3 m·K

Therefore, the peak wavelength is

λ_max = 2.897 x 10^-3 m·K/T

=> λ_max = 2.897 x 10^-3 m·K/5778 K

=> λ_max = 5.01 x 10^-7 K or 501 nm

Therefore, the wavelength of light emitted by the Sun corresponds to the greenish-yellow band of the visible spectrum.

Problem 2. Determine the surface temperature of a star with a peak wavelength of 950 nm.

Solution

Given λ_max = 950 nm

Wien’s law equation is

λ_max x T = 2.897 x 10^-3 m·K

Therefore, the surface temperature of the star is

T = 2.897 x 10^-3 m·K/ λ_max

=> T = 2.897 x 10^-3 m·K/ 950 x 10^-9 nm

=> T = 3049 K