Beer-Lambert Law
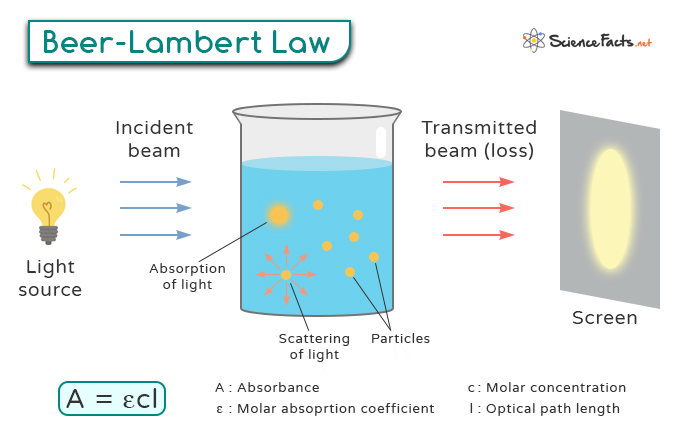
The Beer-Lambert Law is a fundamental principle in physics and chemistry, especially in absorption spectroscopy, that describes the attenuation of light passing through a substance. It provides a mathematical relationship between the substance’s concentration in a solution and its ability to absorb light.
Statement: “The amount of light absorbed by a substance is directly proportional to the substance’s concentration and the path length of light.”
Equation
Let us consider a sample solution with concentration c and path length l. When light passes through this solution, it is absorbed by particles or molecules in the sample. The amount of light absorbed is directly proportional to the concentration and path length.
According to Beer-Lambert Law, we can express this relationship mathematically as:
Where:
– A represents absorbance
– ε (epsilon) is molar absorptivity
– c signifies concentration
– l denotes path length
Absorbance (A) refers to the amount of light absorbed by a sample as it passes through it. It is a dimensionless quantity that is calculated based on the intensity of the incident light (Io) and the transmitted light (I) using the following relationship:
Measuring absorbance involves comparing light intensity before and after interacting with a sample. It is typically done using a spectrophotometer, which emits light of a specific wavelength onto the sample.
Molar absorptivity (ε), also known as molar absorption coefficient or molar extinction coefficient, measures how strongly a substance absorbs light at a specific wavelength. It can vary significantly depending on the wavelength of the incident light. A higher ε value means stronger absorption at that wavelength. The unit of molar absorptivity is liters per mole per centimeter (L mol-1 cm-1).
The path length (l) is the physical distance that the light beam travels through the absorbing medium, typically measured in centimeters (cm). The longer the path length, the more opportunities there are for the light to interact with the sample molecules, leading to higher absorbance.
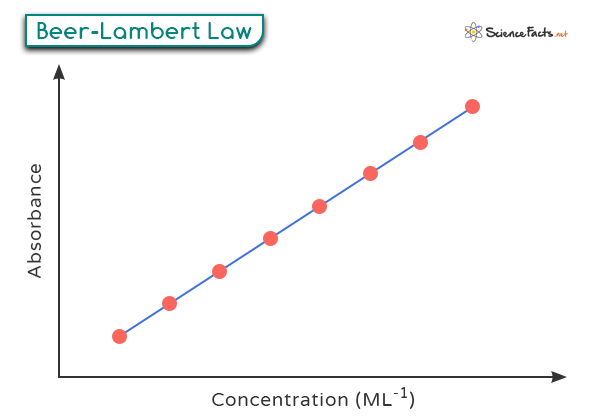
Beer-Lambert Law is graphically represented as follows.
Derivation
1. Determining the Intensity
When a beam of monochromatic light of initial intensity Io passes through a medium, it is partially absorbed by the medium. The decrease in light intensity is proportional to the intensity of the incident light and the path length l through the medium. Mathematically, this relationship is expressed as:
where dI is the infinitesimal decrease in intensity, α is the absorption coefficient, and dx is the infinitesimal path length.
To find the total absorption over a finite path length l, we integrate the above differential equation. Rearranging the terms, we get:
Integrating the left-hand side from Io to I and the right-hand side from 0 to l:
This simplifies to:
Solving for I, we exponentiate both sides:
This shows that light intensity decreases exponentially with the path length in the medium.
2. Relation to Concentration
The absorption coefficient α is proportional to the concentration of the absorbing species c in the medium and the molar absorptivity ε of the species, giving
Substituting this into the exponential equation:
To express the law in a more commonly used form, we take the natural logarithm:
The left-hand side of the above equation is the absorbance A of the medium. Therefore,
Thus, we derived the Beer-Lambert Law in its final form.
Applications
- Spectroscopy: It is used to determine concentrations of various compounds in solutions or identify unknown substances based on their absorption spectra.
- Blood Analysis: It can determine the concentrations of various biomolecules, such as glucose, cholesterol, and hemoglobin, in blood samples.
- Environmental Monitoring: This involves monitoring pollutant levels in water bodies and the atmosphere. Pollutants like nitrates, phosphates, and heavy metals can be determined in water using UV-visible spectrophotometry.
- Food Analysis: It analyzes the concentration of various components in food and beverages. For example, the concentration of caffeine in coffee, sugar in soft drinks, and color additives in food products can be determined spectrophotometrically.
- Drug Analysis: The concentration of active pharmaceutical ingredients (APIs) and impurities is often measured using spectrophotometric techniques, ensuring the efficacy and safety of pharmaceutical products.
Limitations
- It assumes that the sample being measured is in a homogeneous solution. Any deviations from this can lead to inaccurate results. Factors such as solute-solvent interactions and temperature fluctuations can affect the homogeneity of the solution and thus impact the accuracy of measurements.
- This law assumes that all wavelengths are equally absorbed by the solute, which may not always be true. Some substances may have selective absorption at certain wavelengths, leading to deviations from linearity and affecting accuracy.
- It does not consider instrumental limitations. Stray light, detector sensitivity, instrumental noise, and improper calibration and standardization can introduce measurement errors and compromise accuracy.
- It assumes a linear relationship with concentration, which holds for a certain concentration range. If concentrations exceed this range or become too dilute, accurate measurements may not be possible.
-
References
Article was last reviewed on Tuesday, June 10, 2025





I want to use the images of this page (https://www.sciencefacts.net/beer-lambert-law.html) in my research work. Seeking your permissions for the same.
I will acknowledge this in my work.
Yes, you can use our image. Please cite us.