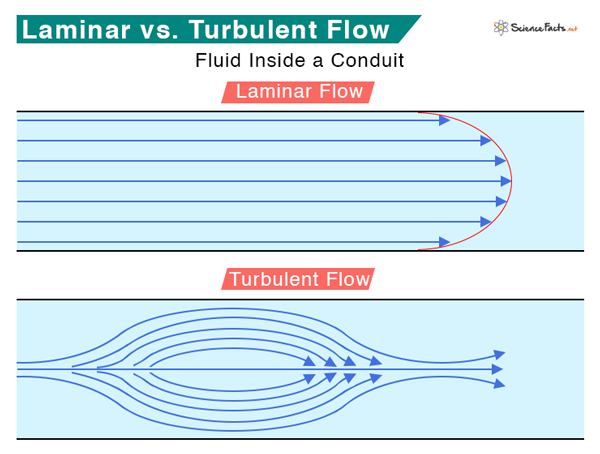
Laminar Flow
Laminar flow is a type of flow in fluids where the motion of the particles is smooth and regular. Unlike turbulent flow, where the movement is irregular, laminar flow is steady and streamlined. Every fluid particle traces an identical trajectory as its preceding particle. Hence, laminar flow is also called streamline flow. One can imagine it to be analogous to playing cards. Typical examples of laminar flow are water flowing out of a faucet and oil flowing through a thin tube.
Characteristics of Laminar flow
In laminar flow, the fluid flow is characterized by different layers that are parallel to one another. Each layer moves smoothly past the adjacent layers with no mixing and disruption between them. The particles in the layers glide smoothly over the adjacent layer. There are no eddies or swirls in laminar flow nor currents perpendicular to the flow. When the fluid flows closer to the surface, the particles move in straight lines parallel to the surface.
Laminar Flow Velocity Profile
Not all fluid particles flow with the same velocity. Layers of fluid flow over one another at different speeds. Laminar flow displays a uniform velocity profile across the conduit. The flow profile can be estimated by dividing the flow into thin cylindrical segments and applying viscous force. The shape of the velocity curve is parabolic for laminar flow. The fluid flowing close to the center of the conduit moves with the highest velocity and consistently decreases as it approaches the walls. The speed can be considered to be zero at the walls.
In many fluid dynamics problems, it is a challenging task to determine the instantaneous velocities at different points on the same cross-section. Therefore, an average value is used in fluid flow equations. This average value of the velocity is obtained by applying integral calculus.
Laminar vs. Turbulent Flow
When a fluid flows through a duct or pipe, the flow could be turbulent or laminar. Two key factors determine the flow – velocity and viscosity.
Laminar flow occurs at low velocity and high viscosity. It is prominent when the diameter of the pipe is small. On the other hand, turbulent flow is characterized by irregular flow with eddies and wakes. Generally, turbulent flow happens at high flow rates and in wide pipes.
There is a threshold value beyond which the flow changes from laminar to turbulent. This value is determined by the Reynolds number, named after British physicist Osborne Reynolds after he popularized its use in 1883. The flow is laminar if the calculated Reynolds number is less than 500. If it is between 500 and 1999, the flow transitions from laminar to turbulent. If it is 2000 and above, the flow is fully turbulent.
Transition Regime
Laminar flow is used to model viscous resistance to flow. However, if the lamina breaks up into turbulence, it will be problematic to characterize the fluid flow. The following table displays the relationship between the Reynolds number (Re) and the regime obtained in different circumstances.
| Situation | Laminar regime | Transition Regime | Turbulent Regime |
|---|---|---|---|
| Flow around a foil parallel to the main flow | Re < 5 x 105 | 5 x 105 < Re < 107 | Re > 107 |
| Flow around a cylinder with the axis perpendicular to the main flow | Re < 2 x 105 | Re ≅ 2 x 105 | Re > 2 x 105 |
| Flow around a sphere | Re < 2 x 105 | Re ≅ 2 x 105 | Re > 2 x 105 |
| Flow inside a circular pipe | Re < 2300 | 2300 < Re < 4000 | Re > 4000 |
Table Courtesy: Simscale.com
Applications
Laminar flow has both industrial and academic applications. In academia, it is widely used in computational fluid dynamics as a benchmark for developing advanced simulation techniques. In industry, a laminar regime is set up in flows with low velocity, low density, and high viscosity. Such a phenomenon is observed in natural convection or ventilation systems working at low speeds.
FAQs
Ans. The blood flow in the vessels can be laminar or turbulent. For instance, a person with high blood pressure has a higher blood flow rate that results in turbulence.
Ans. The friction factor for laminar flow is 64/Re, where Re is the Reynolds number.
-
References
Article was last reviewed on Thursday, June 1, 2023