Velocity
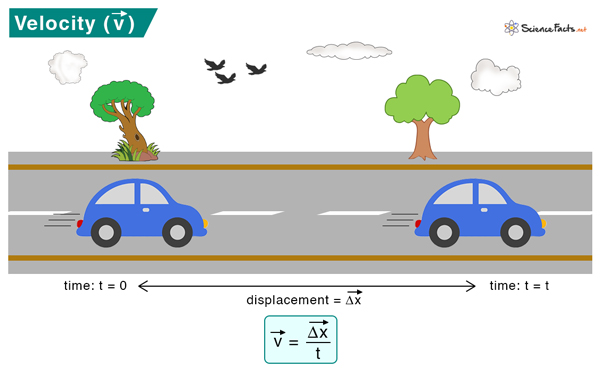
Velocity is the rate at which an object changes position with time. An object is displaced when it changes its position. The amount of displacement over the time in which the displacement occurred gives the velocity. It is a vector quantity that has both magnitude and direction.
The importance of velocity is that it can give you an estimated time to go from one point to another. Suppose you are traveling from place A to place B. Velocity tells you how long it will take to arrive at your destination.
How to Calculate Velocity
Formula
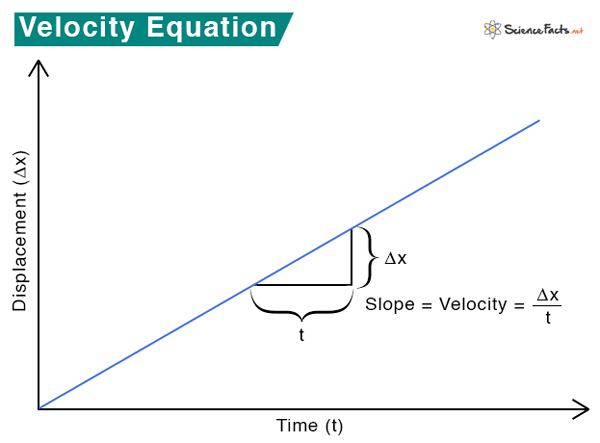
Velocity can be calculated by measuring the object’s displacement over the time taken to displace it.
In vectorial notation, velocity is given by
Units
The SI unit of velocity is Newtons per second of N/s. The cgs unit is ergs per second or ergs/s. Other units include miler per hour or mph, kilometers per hour or kph, and feet per second or fps.
Examples
- A car traveling on the highway at 60 mph toward the West
- A biker riding on the road at 35 mph toward the southwest
- A bicyclist heading northwards at 14 mph
- An airplane flying eastwards at 300 mph
- A rocket launched into the sky in the south-east direction
- A train traveling in the south direction at 80 kph
- A runner runs 420 m in 70 seconds
Average and Instantaneous Velocity
An object can move from one position to another in several steps. The average velocity is simply the change in position over the time interval within which change takes place.
Where,
vavg is the average velocity
xf is the final velocity
xi is the initial velocity
tf is the final time
ti is the initial time
If the starting time is zero, then ti = 0.
The instantaneous (vins.) velocity is the velocity at a particular instant of time. It can be obtained by taking the limit of the above expression in the limit Δt → 0.
Speed vs. Velocity
Both speed and velocity measure rate. Both of them depict how fast an object is moving. However, there is an essential difference. While speed tells us the magnitude of the rate at which the object moves, it does not say anything about the direction. On the other hand, velocity considers the direction of motion.
Let us take an example to illustrate this. When we say a car is moving on the road at 35 mph, we specify the magnitude but not the direction. However, when we say a car is moving on the road eastwards at 35 mph, we specify both the magnitude and direction. The first sentence refers to the speed, and the second refers to the velocity. Therefore, speed is a scalar quantity, and velocity is a vector quantity.
The formula for speed is the distance traveled over the time taken to travel that distance.
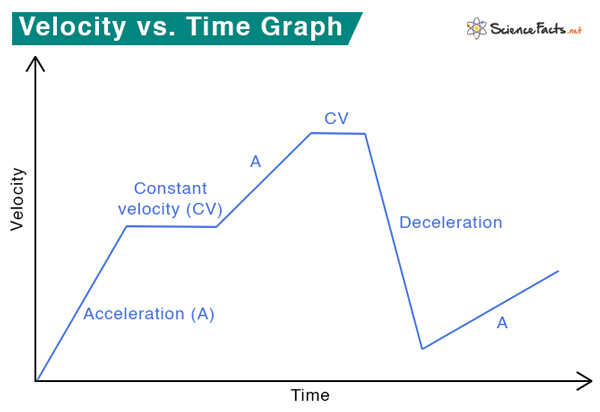
Velocity vs. Time Graph
The following graph shows how velocity changes with time. At some parts of the graph, the velocity increases linearly with time. The quotient of velocity and time is called acceleration. When the velocity decreases with time, the phenomenon is known as deceleration. Regions of constant velocity are also indicated on the graph.
Solved Problems
Problem 1. Suppose a runner moves along the x-direction over some time.During a 5.00 s interval, the runner’s position changes from x1 = 75 m to x2 = 35 m. What was the runner’s average velocity?
Solution
Given x1 = 75 m, x2 = 35 m, Δt = 5 s
The average velocity is given by
vavg = (x2 – x1)/Δt = (35 m – 75 m)/5s = – 8 m/s
Therefore, the runner is running in the negative x-direction.
Problem 2. A commuter train travels from New York to Philadelphia in 1 hour and 25 minutes and from Philadelphia to New York in 1 hour and 35 minutes. The distance between the two stations is approximately 96 miles. What is (a) the average velocity of the train and (b) the average speed of the train in m/s? (1 mile = 1.6 km)
Solution
a) The average velocity of the train is zero since the displacement is zero. (The train returns to New York).
b) Given
d = 96 miles = 96 x 1.6 = 153.6 km = 153.6 x 103 m
t1 = 1 hr 25 mins = 60 mins + 25 mins = 85 mins = 85 x 60 = 5100 s
Therefore, v1 = 153.6 x 103 m / 5100 s = 30.2 m/s
t2 = 1 hr 35 mins = 60 mins + 35 mins = 95 mins = 95 x 60 = 5700 s
Therefore, v2 = 153.6 x 103 m / 5700 s = 26.9 m/s
The average speed is (30.2 m/s + 26.9 m/s)/2 = 28.55 m/s
-
References
Article was last reviewed on Friday, July 28, 2023








on concept of vector
A vector is a physical quantity that has both magnitude and direction.