Perpendicular Axis Theorem

The equation for the perpendicular axis theorem is given by

I_Z = I_X + I_Y

Where I_X, I_Y, and I_Z are the moments of inertia about the x-, y-, and z-axis, respectively.

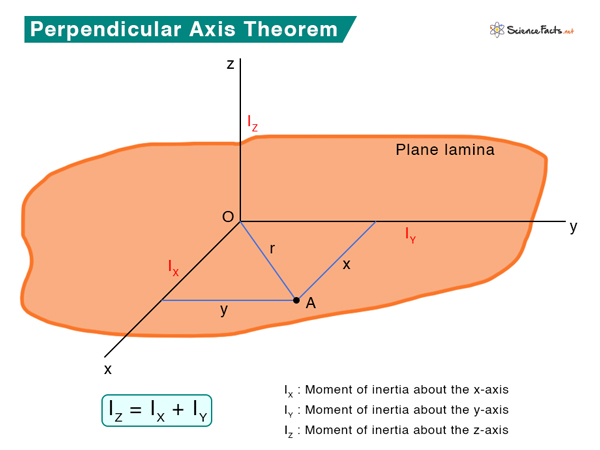
Consider a plane laminar object whose thickness is negligible, as shown in the image above. It is placed on the XY plane such that point O is the origin of the orthogonal coordinate system x, y, and z-axis. Suppose an infinitesimal mass dm lies at point A at a distance r from the origin. This point is at a distance y from the x-axis and x from the y-axis.

The expressions for the moment of inertia about the three axes are given by

Using Pythagoras’ theorem,

r² = x² + y²

Therefore,

I_Z = \(\int \)(x² + y²) dm

=> I_Z = \(\int \)x² dm + \(\int \)y² dm

=> I_Z = I_X + I_Y

Thus, we have proved the perpendicular axis theorem.

The perpendicular axis theorem is applied to calculate the moment of inertia values about perpendicular axes. One can use this theorem to find the moment of inertia values of a few well-known objects from values given in any standard moment of inertia table. Here are some examples.

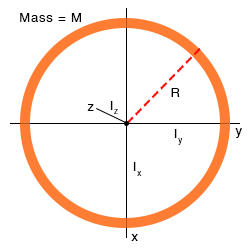
1. Ring

The moment of inertia of a ring of mass M and radius R about the z-axis is

Due to the symmetry of the ring, I_X = I_Y = I. Therefore,

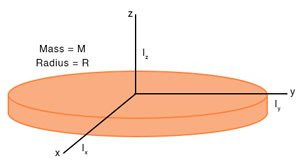
2. Disc

The moment of inertia of a disc of mass M and radius R about the z-axis is given by

Due to the symmetry of the disc, I_X = I_Y = I. Therefore,

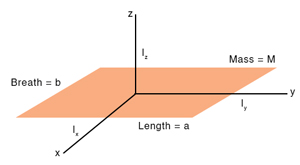
3. Rectangular Section

The moment of inertia of a rectangular section of mass M, length a, and breath b about an axis passing through its center and parallel to its length is

Similarly, the moment of inertia about an axis passing through the center and parallel to the breath is

Using the perpendicular axis theorem

Problem 1. The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod and passing through its center is I. What is the moment of inertia of the rod about an axis in the rod’s plane and perpendicular to it?

Solution

Let the center of the rod be at the origin. Suppose the rod is in the XY plane and along the x-axis. Then, the z-axis is perpendicular to the rod, and the moment of inertia about the z-axis is

I_Z = ML²/12

Using the perpendicular axis theorem

I_Z = I_X + I_Y

Since the rod is thin, its rotation about its axis can be neglected; that is, I_X = 0

Therefore,

I_Z = I_Y

=> I_Y = ML²/12

Problem 2. Suppose the rod in problem 1 has a mass of 1.5 kg and a length of 70 cm. What are the moments of inertia about the x, y, and z axes?

Solution

Given M = 1.5 kg and L = 70 cm = 0.7 m

The moment of inertia values are

I_X = 0

I_Y = I_Z = ML²/12 = (1.5 kg) (0.7 m)/12 = 0.735 kgˑm²