Moment of Inertia

Moment of inertia, also known as rotational inertia or angular mass, is a physical quantity that resists a rigid body’s rotational motion. It is analogous to mass in translational motion. It determines the torque required to rotate an object by a given angular acceleration. Moment of inertia does not restrict itself to a rigid body only. It also applies to a system of particles rotating about a common axis.

How to Calculate Moment of Inertia

Point Mass

For a point mass (single body), the moment of inertia formula is given by the product of mass and the square of the object’s perpendicular distance from the axis of rotation.

\[ I = mr^2 \]

Where

I is the moment of inertia

m is the mass

r is the perpendicular distance from the axis of rotation

System of Particles

Suppose n particles of masses m₁, m₂, …, m_n rotate about a common axis at perpendicular distances r₁, r₂, …, r_n from the axis. Then the moment of inertia of the system is

\[ I = \sum m_i r_i\hspace{0.01 cm}^2 \]

The moment of inertia of a system of particles is the sum of the moments of inertia of the individual particles taken about a common axis.

Units and Dimensions

The SI unit of moment of inertia is kgˑm², and the cgs unit is gˑcm². The dimension is [M L²T⁰].

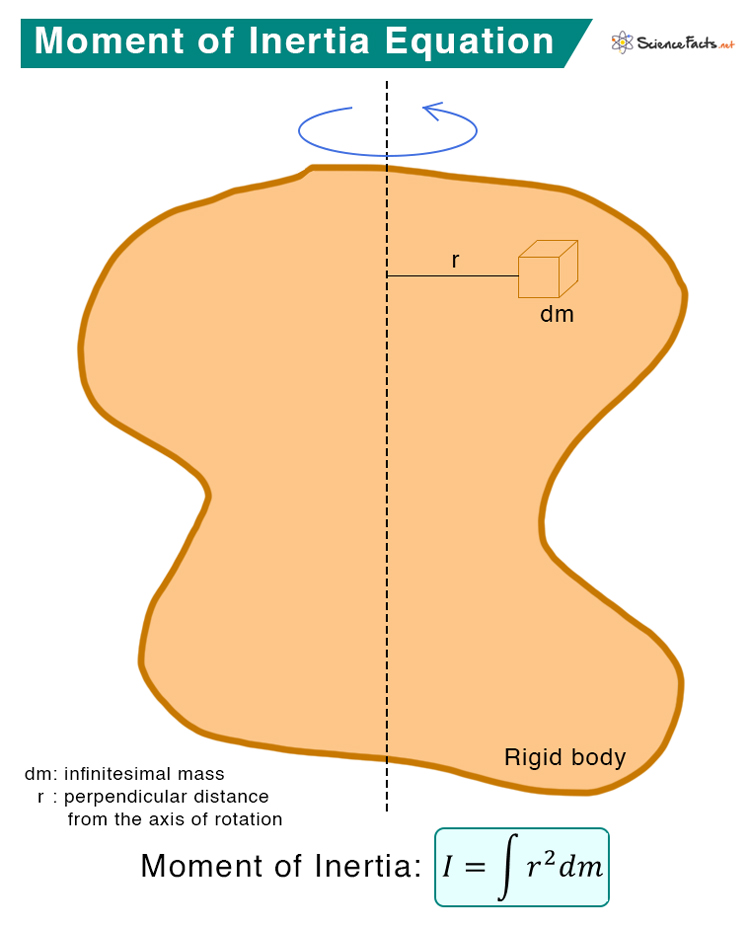
Integral Moment of Inertia

For a continuous mass distribution, the integral form of moment of inertia is given by

\[ I = \int r^2 dm \]

Where dm is the instantaneous mass.

The above equation can also be written in terms of density ρ and instantaneous volume dV as follows.

\[ I = \int r^2 \rho dV \]

Moment of Inertia Table

Several everyday objects, such as rotating disks, cylinders, and spheres, have well-defined moment of inertia formulas. A chart consisting of the different formulas is listed in the table below. Here M represents mass, R represents radius, and L represents the length.

Object	Moment of Inertia Formula	Object	Moment of Inertia Formula
Solid Sphere	(2/5)MR²	Rectangular plate with sides of length a and breath b and axis passing perpendicularly through the center	(1/12)M(a² + b²)
Hollow Thin-Walled Sphere	(2/3)MR²	Rectangular plate with sides of length a and breath b and axis passing perpendicularly through the edge	(1/3)Ma²
Solid Cylinder	(1/2)MR²	Rectangular plate with sides of length a and breath b and axis passing parallelly through the center	(1/12)Ma²
Hollow Thin-Walled Cylinder	MR²	Slender rod with the axis through the center	(1/12)ML²
Hollow Cylinder, with inner radius R₁ and outer radius R₂	(1/2)M(R₁² + R₂²)	Slender rod with the axis through one end	(1/3)ML²

Moment of Inertia and Rotational Kinematics

The moment of inertia of a rotating object about a fixed axis is useful in calculating a few key quantities in rotational motion. Newton’s second law for rotation gives a relationship between torque, moment of inertia, and angular acceleration. According to this law,

\[ \tau = I\alpha \]

Where

τ is the applied torque

I is the moment of inertia

α is the angular acceleration

The relationship between moment of inertia and rotational kinetic energy is given by

\[ K = I \omega^2 \]

And with angular momentum, the equation is

\[ L = I\omega \]

Where

K is the rotational kinetic energy

L is the angular momentum

ω is the angular velocity

Factors Affecting Moment of Inertia

The moment of inertia depends upon

The shape of the object
Mass distribution or density
Location of the axis of rotation

References
- 1. Moment of Inertia – Hyperphysics.phy-astr.gsu.edu
  2. Rotational Inertia – Khanacademy.org
  3. Moment of Inertia – Isaacphysics.org
  4. What Is Moment of Inertia in Physics? – Thoughtco.com
  5. Center of Mass; Moment of Inertia – Feynmanlectures.caltech.edu
  6. Calculating Moment of Inertia – Phys.libretexts.org