Compton Scattering (Compton Effect)

Compton scattering is a fundamental process in physics that describes the interaction between a photon and an electron. This phenomenon occurs when a high-energy photon collides with an electron, resulting in the photon losing some of its energy. When a photon interacts with an electron, it transfers some of its energy to the electron. This transfer causes the photon to change its wavelength and direction, resulting in scattering.

Compton scattering played a crucial role in confirming the particle nature of light. This process was first explained by American physicist Arthur Holly Compton in 1923, who demonstrated that light behaves as both particles (photons) and waves.

Equation

Energy and momentum must be conserved when a photon collides with an electron. The Compton scattering equation relates the photon’s wavelength change to the scattering angle and the electron’s rest mass.

The equation is written as:

\[ \Delta \lambda = \lambda^\prime – \lambda = \frac{h}{m_e c} (1 – \cos \theta ) \]

Where:

Δλ is the change in wavelength of the photon

λ’ is the wavelength of the scattered photon

λ is the wavelength of the incident photon

h is Planck’s constant

m_e is the rest mass of the electron

c is the speed of light

The scattering angle θ represents the angle between the incident and the scattered photon’s direction. This equation demonstrates that a shift in wavelength occurs due to the interaction between the photon and electron.

Derivation

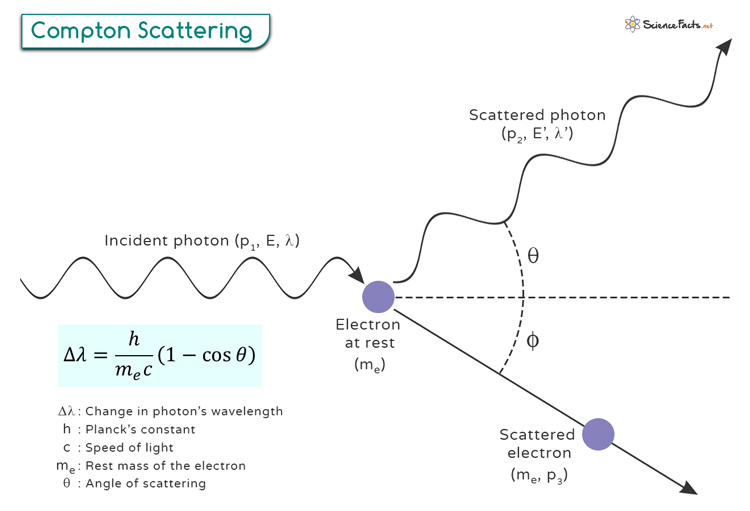
The derivation of the Compton scattering formula involves applying conservation laws and principles of relativistic mechanics. Let us look at the image below and understand the various quantities involved.

p₁ and E are the photon’s initial momentum and energy, respectively.

p₂ and E’ are the photon’s final momentum and energy, respectively.

m_e and p₃ are the electron’s rest mass and final momentum, respectively.

θ is the angle by which the photon scatters.

φ is the angle by which the electron recoils.

We assume that the photon initially moves along the x-direction so that only the x and the y components of the momentum will be considered in our derivation.

Conservation of momentum along the x- and y- directions gives rise to the following equations.

p₁ = p₂ cos θ + p₃ cos φ (x-direction)

p₂ sin θ = p₃ sin φ (y-direction)

According to the conservation of energy, the total energy before the interaction is given by E + m_ec². After the scattering, the photon loses energy and momentum while the electron gains the same. Conservation of energy gives us the following relativistic equation.

\[ E + m_e c^2 = E’ + \sqrt{p_3^{\hspace{0.1 cm}2} c^2 + m_e^{\hspace{0.1 cm}2} c^4} \]

We aim to solve for E’ in terms of cos θ and eliminate φ in the process. Continuing from the energy equation, we get

\[ E -E’ + m_e c^2 = \sqrt{p_3^{\hspace{0.1 cm}2} c^2 + m_e^{\hspace{0.1 cm}2} c^4} \]

Squaring both sides

\[ (E -E’ + m_e c^2)^2 = (\sqrt{p_3^{\hspace{0.1 cm}2} c^2 + m_e^{\hspace{0.1 cm}2} c^4})^2 \\ => E^2 -E’^2 + m_e^{\hspace{0.1 cm}2} c^4 – 2 EE’ – 2E’m_ec^2 + 2 Em_ec^2= p_3^{\hspace{0.1 cm}2} c^2 + m_e^{\hspace{0.1 cm}2} c^4 \]

We need to replace p₃ and use the momentum conservation equations.

(p₃ cos φ)² = (p₁ – p₂ cos θ)²

(p₃ sin φ)² = (p₂ sin θ)²

Adding the two equations, we get

p₃² = p₁² + p₂² – 2 p₁p₂ cos θ

Back to the energy equation

\[ E^2 -E’^2 + m_e^{\hspace{0.1 cm}2} c^4 – 2 EE’ – 2E’m_ec^2 + 2 Em_ec^2= p_1^{\hspace{0.1 cm}2} c^2 + p_2^{\hspace{0.1 cm}2} c^2 – 2 p_1p_2 \cos \theta \hspace{0.1 cm}c^2+ m_e^{\hspace{0.1 cm}2} c^4 \\ => E^2 -E’^2 – 2 EE’ – 2E’m_ec^2 + 2 Em_ec^2= p_1^{\hspace{0.1 cm}2} c^2 + p_2^{\hspace{0.1 cm}2} c^2 – 2 p_1p_2 \cos \theta \hspace{0.1 cm}c^2 \]

Using the photon-energy equation E = pc, we can rewrite the energy equation as

\[ E^2 – E’^2 – 2 EE’ – 2E’ m_e c^2 + 2 E m_e c^2= E^2 + E’^2 – 2 EE’ \cos \theta \\ => 2 m_e c^2 (E – E’) = 2 EE’ (1 – \cos \theta ) \]

Using the relationship between energy and momentum for a photon, E = hc/λ, where h is Planck’s constant and λ is the wavelength, we can rewrite the equation as

\[ 2 m_ec^2 \left( \frac{hc}{\lambda} -\frac{hc}{\lambda^{\prime} } \right) = 2\frac{hc}{\lambda}\frac{hc}{\lambda ^{\prime}} (1- \cos \theta ) \\ => \frac{1}{\lambda} -\frac{1}{\lambda ^{\prime}} = \frac{h}{m_e c} \frac{1}{\lambda \lambda ^{\prime}} (1 – \cos \theta) \\ => \Delta \lambda = \lambda ^{\prime} -\lambda = \frac{h}{m_e c} (1 – \cos \theta) \]

Which is the Compton wavelength shift equation for the photon.

The minimum change in wavelength occurs when θ = 0° or cos θ = 1, resulting in Δλ = 0. The maximum change in wavelength occurs when θ = 180° or cos θ = -1, resulting in Δλ = 2h/m_ec. In this case, the photon transfers to the electron as much momentum as possible. The value of this maximum change is

\[ (\Delta \lambda)_{max} = \frac{2h}{m_e c} = \frac{2 \times 6.626 \times 10^{-34} \hspace{0.01 cm} \text{J} \cdot \text{s}}{9.1 \times 10^{-31} \hspace{0.01 cm} \text{kg} \times 3 \times 10^8 \hspace{0.01 cm} \text{m} \cdot \text{s}^{-1}} = 4.85 \times 10^{-12} \hspace{0.01 cm} \text{m} \]

The quantity h/m_ec is known as the Compton wavelength of the electron and is equal to 2.43 x 10^-12 m.

Applications

Compton scattering finds applications in various fields, such as astronomy, medical imaging, and nuclear physics. It plays a crucial role in understanding X-ray diffraction and gamma-ray astronomy. It helps scientists study the properties of matter, understand the behavior of radiation, and gather information about the structure and composition of materials.

Inverse Compton Scattering

When the electron is not at rest but has an energy greater than the typical photon energy, there can be a transfer of energy from the electron to the photon. This process is called inverse Compton scattering to distinguish it from direct Compton scattering, in which the electron is at rest, and the photon gives some energy to the electron. This energy exchange results in the emission of a new photon with a higher energy than the incoming photon. This phenomenon is the reverse of the Compton scattering process. It is applied in nuclear physics and astrophysics.

Compton Effect vs. Photoelectric Effect

Both Compton and photoelectric effects obey the conservation of momentum and energy. Here is a table highlighting the key differences between the Compton effect and the photoelectric effect:

Property	Compton Effect	Photoelectric Effect

Description	Scattering of photons by electrons	Ejection of electrons by photons
Interaction	Involves the interaction of X-rays or gamma rays with electrons	Involves the interaction of photons (typically ultraviolet or visible light) with electrons
Energy Transfer	Results in the scattering of incoming photons with a change in their energy (wavelength)	Leads to the emission of electrons from a material surface when photons are absorbed
Dependency on Photon Energy	The change in photon energy is proportional to the incident photon’s energy and the scattering angle.	The photoelectric effect is most efficient when incident photons have energy above a material-specific threshold, known as the work function.
Applications	Important in astrophysics for understanding gamma-ray production and X-ray sources	Essential in the development of photodetectors, solar cells, and photomultiplier tubes

References
- 1. Compton Scattering – Hyperphysics.phy-astr.gsu.edu
  2. Compton Effect – Eng.libretexts.org
  3. Compton Effect – Wanda.fiu.edu
  4. What the Compton Effect Is and How It Works in Physics – Thoughtco.com
  5. Compton Scattering – Nuclear-power.com