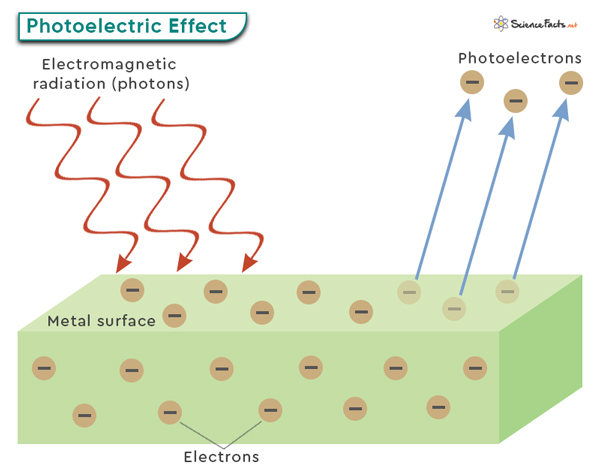
Photoelectric Effect
The photoelectric effect refers to the phenomenon where light, typically in the form of photons, can cause the emission of electrons from a material’s surface. In simple terms, when light shines on a material, it can transfer its energy to electrons within the material. If this energy is sufficient, the electrons can overcome the attractive forces holding them to the material and eject as free particles. These emitted electrons are referred to as photoelectrons.
Who Discovered Photoelectric Effect
The photoelectric effect was discovered in 1887 by German physicist Heinrich Rudolf Hertz while working on relevant radio waves. Noted physicist Albert Einstein explained the phenomenon in 1905, for which he got the Nobel Prize in 1921. It has since become a key concept in understanding the behavior of light and electrons.
Photoelectric Effect Explained
Einstein’s explanation of the photoelectric effect revolutionized our understanding of light and laid the foundation for developing quantum physics. In 1905, Einstein proposed that light comprises tiny packets of energy called photons. He suggested that when light interacts with matter, each photon transfers its energy to an electron in the material.
The photoelectric effect is typically observed with metals, as they have loosely bound or delocalized electrons that are more easily excited by incoming photons. However, it can also occur with other materials like semiconductors or insulators under specific conditions.
A critical aspect of the photoelectric effect is that it follows specific principles. First, there is a minimum energy threshold that the incident photons must have to cause electron emission. This threshold energy is directly related to the material’s work function.
Additionally, the intensity or brightness of the incident light does not affect the kinetic energy of emitted electrons but rather determines their number or intensity. On the other hand, changing the frequency or color of light can alter the kinetic energy of photoelectrons.
Equation for Photoelectric Effect
One can analyze the photoelectric effect by using the energy conservation law. The total energy of the incoming photon must be equal to the kinetic energy of the ejected electron plus the energy required to eject the electron from the metal. It is described mathematically by the photoelectric equation:
E = φ + KE
The components of this equation are as follows:
- Energy of a photon (E): It represents the energy carried by a single photon of light. It is directly proportional to the frequency (v) of the light wave and can be calculated using the equation E = hv, where h is Planck’s constant (= 6.62 x 10-34 Jˑs)
- Work function (φ): It refers to the minimum amount of energy required to remove an electron from a specific material.
- Kinetic energy of the ejected electron (KE): It represents an electron’s kinetic energy after emitting from the material.
By rearranging the above equation, one can determine the ejected electron’s kinetic energy.
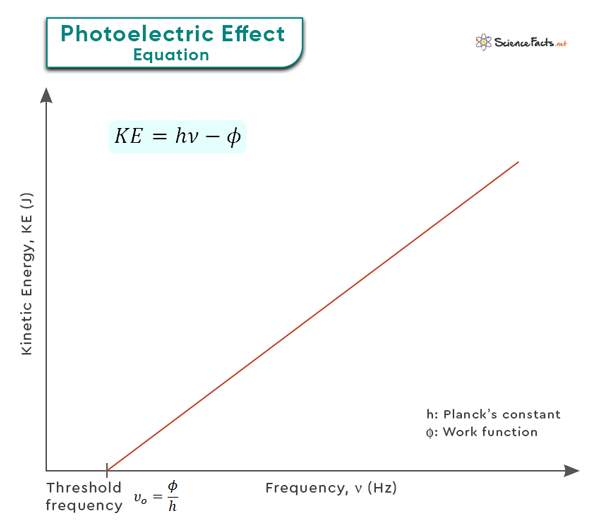
KE = hν – φ
This equation emphasizes the direct relationship between the energy of incident photons and the photoelectron’s energy required to overcome the work function. It also demonstrates that electrons are only emitted when the energy of the incident photons is greater than the work function.
We can also use this equation to find the photoelectron velocity (v), which is related to its mass and kinetic energy as follows:
KE = ½ mev2
Therefore,
½ mev2 = hν – φ
Where me is the rest mass of the electron (= 9.1 x 10-31 kg).
Problem: What is the velocity of photoelectrons ejected from copper metal by an electromagnetic wave of frequency 4.0 x 1016 Hz? The work function of copper is 7.53 x 10-19 J.
Given: ν = 4.0 x 1016 Hz, φ = 7.53 x 10-19 J
We use the following equation:
½ mev2 = hν – φ
=> ½ x 9.1 x 10-31 kg x v2 = 6.62 x 10-34 Jˑs x 4.0 x 1016 s-1 – 7.53 x 10-19 J
=> v = 7.52 x 106 mˑs-1
Therefore, the electron moves with a velocity of 7.52 x 106 meters per second.
Note that the kinetic energy of the photoelectron increases linearly with frequency as long as the photon energy is greater than the work function, precisely the relationship shown in the graph below.
Work Function
The work function serves as a crucial parameter in understanding the photoelectric effect. It is a fundamental property of a material and determines how easily electrons can be ejected from it. The work function is influenced by various factors, including the nature of the material, its crystal structure, and temperature.
Different materials have different work functions, ranging from a few electron volts for metals to several for insulators. Materials with lower work functions are more susceptible to the photoelectric effect and emit electrons more readily when exposed to light.
Understanding and manipulating the work function is essential for various applications. For example, solar cells should have a low work function at the electrode interfaces to facilitate efficient electron transfer. Additionally, controlling and optimizing the work function is crucial for achieving desired electrical properties in transistors and diodes.
Application
The photoelectric effect has numerous applications in various fields, including photoelectrochemical cells and solar energy conversion. Here is a brief overview of their significance:
- Photoelectrochemical Cells: These cells use the photoelectric effect to convert light energy into chemical energy. They consist of a semiconductor electrode that absorbs light and generates electron-hole pairs, which then participate in electrochemical reactions. Photoelectrochemical cells have significant applications in water splitting, fuel generation, and environmental remediation.
- Solar Energy Conversion: Understanding the photoelectric effect is crucial for developing and improving solar energy technologies. Photovoltaic (PV) cells, or solar cells, utilize the photoelectric effect to convert sunlight directly into electricity. By absorbing photons from sunlight, PV cells generate a flow of electrons, which can be harnessed for various applications, including powering homes, buildings, and even entire cities.
-
References
Article was last reviewed on Tuesday, September 19, 2023