Coulomb’s Law
What is Coulomb’s Law
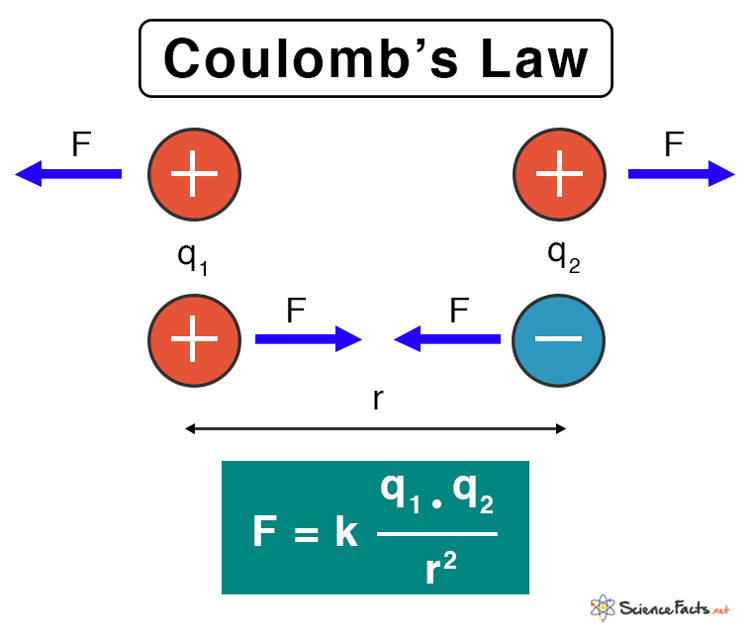
All charged particles attract or repel one another depending upon their nature. Generally, like charges repel and unlike charges attract. Coulomb’s law determines the electrostatic force of attraction or repulsion between them. The law is usually applied to point charges. It gives a relationship between the electrostatic force, the magnitude of the charges, and the separation distance.
Statement of Coulomb’s Law
Coulomb’s law states that the electrostatic force between the two particles is
- Directly proportional to the product of the magnitude of the charges
- Inversely proportional to the square of the distance between the two charges
This law is named after French physicist Charles-Augustin de Coulomb, who published it in 1785.
Coulomb’s Law Equation
Scalar Form
Suppose two point charges are separated by a certain distance. Then, according to Coulomb’s law, the electrostatic force, also known as Coulomb’s force, between the two charges is given by the following formula.
Where,
F: Electrostatic force
k: Coulomb’s constant
q1, q2: Magnitude of the point charges
r: Distance of separation between the charges
SI Unit: Newton or N
Dimension: [M L T-2]
Because of the inverse relationship, this law is sometimes called Coulomb’s inverse square law.
Vector Form
The vector form of Coulomb’s law is given by,
Where,
Coulomb’s Law Constant
The constant in Coulomb’s law is known as Coulomb’s constant, which is denoted by k. Suppose, q1 = 1, q2 = 1, and r = 1, then,
Therefore, Coulomb’s constant is defined as the electrostatic force experienced by two unit charges when a unit distance separates them. It is expressed as follows.
In free space,
In a medium,
Where,
εo: Permittivity of free space or vacuum (= 8.85 x 10-12 C2N-1m-2)
εr: Permittivity of the medium
The ratio of εr and εo is known as the relative permittivity of the medium or dielectric constant.
Dielectric Constant: κ = εr/εo
Putting the value of εo gives the value of k,
Coulomb’s Constant: 9 x 109 Nm2C-2
Using the expression for k, the Coulomb’s Law equation in free space is given by,
Superposition Principle of Coulomb’s Law
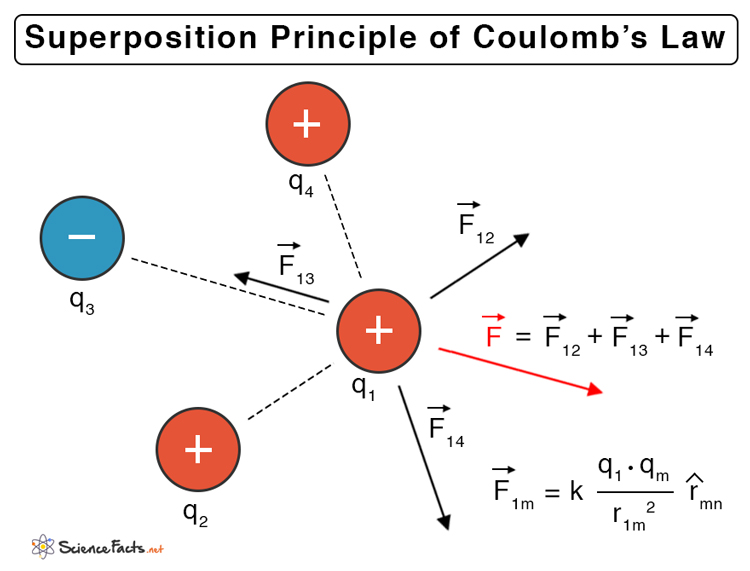
Coulomb’s law refers to the interaction between two point charges. For more than two charges, the force on each charge due to the presence of other charges should be taken into account. Since force is a vector quantity, the superposition principle must be applied.
According to the superposition of forces, all linear forces can be added vectorially. The net force is the vectorial sum of all the individual forces. Consider a system of n charges given by q1, q2, …, qn, the force due to charges q1 and q2 is,
Where,
Similarly, the force between q1 and any other charges are,
Therefore, the net force due to q1 is,
Limitations
- Applicable only to point charges at rest
- Applicable to cases where inverse-square law is obeyed
- It cannot be applied to irregular-shaped charges
- It cannot be applied to a continuous charge distribution
Applications
- To calculate the force between two charges
- To calculate the distance between two charges
- To study the motion of electrons around an orbit in an atom
- To calculate the electrostatic potential and hence the work done in moving a charge from one point to another
- To calculate the relative permittivity (dielectric constant) of a medium
- Inkjet printers use electrostatic forces to spray tiny ink droplets, which are charged when passing through a nozzle
- Photocopiers and laser printers use an electrostatic process in which an electrically charged drum coated with selenium attracts a blank piece of paper to print images
Other applications include power coating and electrostatic air cleaning
Examples and Practice Problems
Problem 1. Two identical charges -6.25 nC are held apart at a separation distance of 42 cm. Determine the magnitude of the electrical force of repulsion between them.
Solution:
Given,
q1 = 6.25 nC
q2 = 6.25 nC
r = 42 cm = 0.42m
We have,
F = k q1 q2 /r2
= (9 x 109 Nm2C-2 x 6.25 nC x 6.25 nC)/0.422 m2
= 2 μN
Problem 2. The force between two identical charges separated by 2 cm is equal to 45 N. What is the magnitude of the two charges?
Solution:
Given,
F = 45 N
d = 2 cm = 0.02 m
q = q1 = q2
We have,
F = k q1 q2 /r2
= k q2/r2
Or, q = sqrt (F r2/k)
= sqrt (45 N x (0.02 m)2/ 9 x 109 Nm2C-2)
= 1.41 μC
Problem 3. Two balloons with charges of +4 µC and -8 µC attract each other with a force of 0.0625 N. Determine the separation distance between the two balloons.
Solution:
Given,
F = 0.0625 N
q1 = 4 μC = 4 x 10-6 C
|q2|= 8 μC = 8 x 10-6 C
We have,
F = k q1 q2 /r2
Or, r = sqrt (k q1 q2 / F)
= sqrt (9 x 109 Nm2C-2 x 4 x 10-6 C x 8 x 10-6 C/0.0625 N)
= 2.15 m
Problem 4. Two neutrally charged bodies are separated by 0.5 cm. Electrons are stripped off from one body and placed on the second body until a force of 2 μN is generated between them. How many electrons were transferred between the bodies?
Solution.
Given,
q1 = +ne
q2 = -ne
e = 1.6 x 10-19 C
r = 0.5 cm = 5 x 10 -3 m
F = 2 μN = 2 x 10-6 N
We have,
F = k q1 q2 /r2
Or,|F| = k n2e2 /r2
Or, n = sqrt (F r2 / k e2)
= sqrt (2 x 10-6 N x (5 x 10 -3 m)2 / (9 x 109 Nm2C-2 / (1.6 x 10-19 C)2))
= 6.5 x 108
-
References
Article was last reviewed on Friday, February 3, 2023








Sir make this website as a android app for better Reading…Sir tell me this website Android app if it is available..
We do not have an app for this site. I think you should be able to read it clearly using any browser on the phone.