Displacement
Displacement is the change in an object’s position relative to a reference frame. For example, when a player strikes a billiards ball, the ball moves from one position to another. It is said to be displaced. Displacement is a vector quantity that has both magnitude and direction.
Examples
- A plane flying from New York to London
- A jogger running along a curve path from north to south in a park
- A cross-country skier skiing for 6 hours on a designated track
- Children playing and running around in circles
- A marching band walking in a straight line across a football field
How to Calculate Displacement
To determine displacement, one must know the object’s position in a frame of reference or coordinate system. We use the distance from a reference point to represent the position. In a coordinate system, that reference point is called the origin.
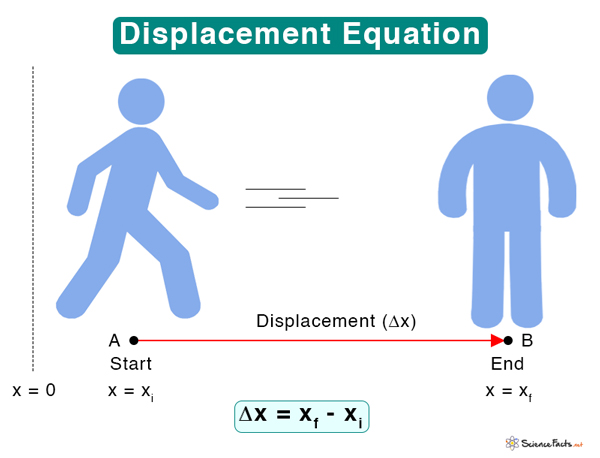
Consider a one-dimensional coordinate system. The variable x is often used to indicate position. Suppose a person is at position A, at a distance xi from the origin. Here, the subscript i refers to the initial position. After some time, he moves to position B at a distance xf from the origin, where f refers to the final position. Then, the displacement (Δx) of the person is
Δx = xf – xi
SI Unit: Meter or m
Can Displacement be Negative
From the above equation, it is clear that if xf > xi, Δx > 0. In other words, the displacement is positive. However, if xf < xi, Δx < 0, the displacement is negative. Therefore, the displacement can be negative depending upon the person’s initial and final positions, which in turn, depends on the direction in which he moves. In this case, he moves right in the positive x-direction. So, his displacement is positive. Had he moved left in the negative x-direction, the displacement would have been negative.
Magnitude and Direction
The magnitude of displacement is given by
|Δx| = |xf – xi|
The red arrow in the above images indicates the direction of displacement.
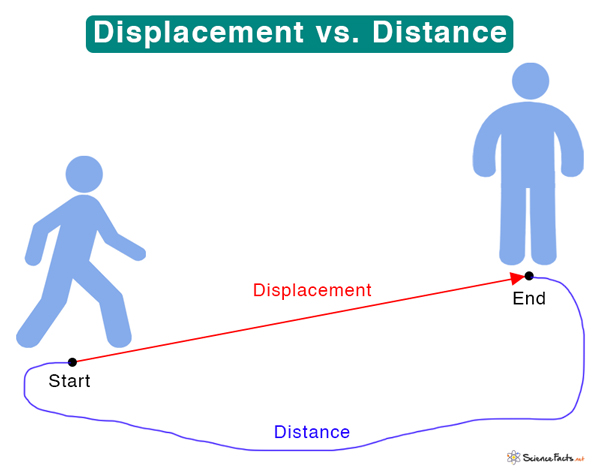
Displacement and Distance
Distance refers to the total ground covered by an object while moving from one point to another. It is a scalar quantity that is also measured in meters.
Suppose a person walks from point A to B, not in a straight line but through a curved path. The blue curve illustrates his movement in the image below. In other words, the person has changed his direction multiple times while traversing from A to B. The blue path indicates the distance he covered, and the straight red arrow indicates his displacement.
The following table highlights the difference between the two.
| Property | Distance | Displacement |
|---|---|---|
| Definition | The total path length between any two points | The direct path length between any two points (We use the idiom “as the crow flies” to describe displacement) |
| Scalar or Vector | Scalar | Vector |
| Positive or Negative | Positive | Positive, negative, and zero |
Displacement Graphs
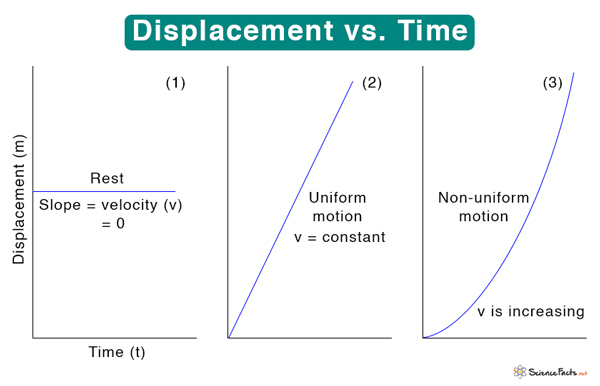
A displacement graph usually shows the displacement as a function of time. Here, displacement is the dependent variable and is represented on the y-axis. On the other hand, time is the independent variable and is represented on the x-axis. The ratio of displacement over time gives the velocity. There are three different plots for the displacement vs. time graph, which are shown in the image below.
Plot (1) shows that the object remains stationary for a while. In other words, the displacement is constant, and the slope is zero. The velocity of the object is zero.
Plot (2) shows that the displacement varies linearly with time. The slope of the graph, and hence the velocity, remains constant and positive.
Plot (3) shows that the displacement increases nonuniformly with time. It means that the slope and velocity increase with time. Since the velocity is increasing, the object is displaying acceleration.
-
References
Article was last reviewed on Friday, November 18, 2022