Electric Flux

What is Electric Flux

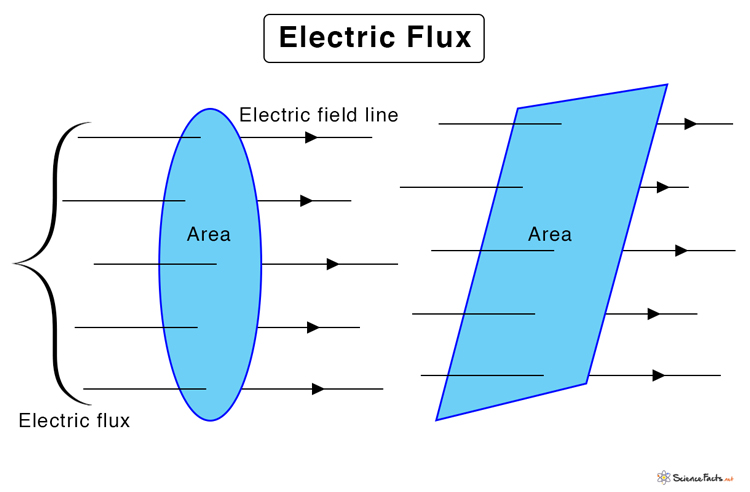
The number of electric field lines or electric lines of force passing through a given surface area is called electric flux. The area can be in air or vacuum. It can also be inside or on the surface of a solid conductor. The number of lines passing per unit area gives the electric field strength in that region.

Electric Flux Equation

All flat surfaces have an area associated with them. A regular geometric surface like a circle, rectangle, square, or triangle has a well-defined area. Mathematically, a surface is represented by a vector known as an area vector, whose magnitude is the quantified area, and the direction is perpendicular to the surface.

\[ \vec{A} = A\hat{n} \]

Where,

\[ \vec{a} \text{: Area vector}\\ \vec{A} \text{: Magnitude of the area} \\ \hat{n} \text{: Unit vector perpendicular to the surface} \]

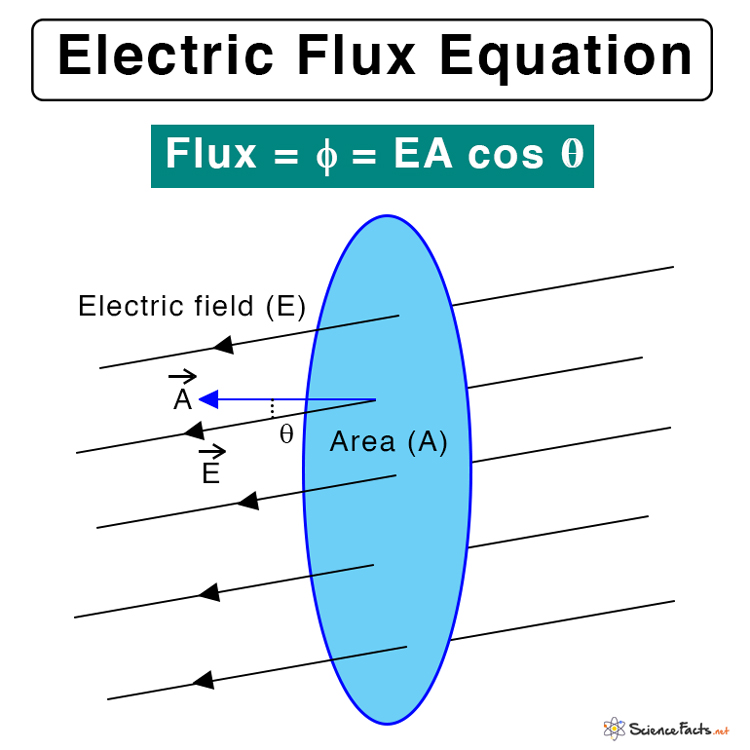
Mathematically, the electric flux is given by the dot product of the electric field vector and area vector.

\[ \phi = \vec{E}.\vec{A} \]

Where

\[ \phi \text{: Electric flux}\\ \vec{E} \text{: Electric field}\\ \vec{A} \text{:Area vector} \]

If the angle between the electric field vector and the area vector is θ, then the dot product can be expanded to give the magnitude of electric flux.

\[ \phi = EA\cos \theta \]

Symbol: φ or phi

SI Unit: Volt-meter (V-m) or Newton per meter-squared per Coulomb (Nm²C^-1)

CSG Unit: stat Coulomb (statC) or Franklin (Fr) (1 C = 3 x 10⁹ statC)

Dimension: [M L³ T⁻³ A⁻¹]

When θ = 0˚, cos 0˚ = 1, therefore, φ = EA

Therefore, the maximum number of electric field lines will pass through a surface placed perpendicular to the electric field. The electric flux can be negative if the electric field vector and the area vector are in opposite directions.

Electric Flux Density

The electric flux density is the number of electric field lines passing through a unit area projected perpendicular to the flow direction. Consider the flux equation.

\[ \phi = EA \]

For unit area, A = 1.

\[ \phi = E \]

Therefore, the electric flux density is equal to the magnitude of the electric field.

Integral Form

The above equation applies to situations where the electric field is uniform and the surface is flat. If the electric field changes in magnitude and/or direction over the entire surface, then it is non-uniform. For a non-uniform electric field and curved surface, the electric flux is determined by integrating the dot product over the surface. For this purpose, an infinitesimal area is taken. The electric flux is given by the equation

\[ \phi = \int \vec{E}.\vec{dA} \]

Where dA = dA n

\[ \vec{dA} = dA \hspace{0.1 cm} \hat{n} \text{ is the infinitesimal area vector} \]

Consider a curved surface like a sphere, cube, or cylinder. In this case, the integration is carried over the curved surface. We will see this in the examples below.

Electric Flux Through a Sphere

Consider the electric field lines originating from a point charge. According to Coulomb’s law, the electric field E due to a point charge q at a distance r is given by,

\[ E = \frac{q} {4\pi \epsilon_o r^2} \]

From the above equation, it is pretty clear that the electric field varies inversely with the square of the distance. Hence, the field is non-uniform. Therefore, to calculate flux passing through a sphere, we have to integrate the field over the sphere’s surface.

Consider an infinitesimal area perpendicular to the sphere’s surface. From the symmetry of the problem, the electric field is radially outwards. Hence, its direction is perpendicular to the surface. Therefore, the angle between the electric field and the infinitesimal area is zero.

\[ \vec{E}.\vec{dA} = E\hspace{0.1 cm}dA \cos 0^o = E\hspace{0.1 cm} dA\]

Also, the infinitesimal area of a sphere is given by

\[ dA = r^2 \hspace{0.1 cm} \sin \theta \hspace{0.1 cm} d\theta \hspace{0.1 cm} d\phi \]

Where r, θ, and φ are the spatial coordinates in a spherical coordinate system.

The electric flux enclosed by a sphere is

\[ \phi = \int \vec{E}. d\vec{A} \\ \implies \phi = \int \frac{q}{4\pi \epsilon_{o} r^2} \hspace{0.1 cm} r^2 \hspace{0.1 cm} \sin \theta \hspace{0.1 cm} d\theta \hspace{0.1 cm} d\phi \\ \implies \phi = \frac{q}{4\pi \epsilon_o } \int \sin \theta \hspace{0.1 cm} d\theta \hspace{0.1 cm} d\phi \\ \implies \phi = \frac{q}{4\pi \epsilon_o } 4\pi \\ \implies \phi = \frac{q}{\epsilon_o } \]

Where,

ε_o = permittivity of free space (= 8.85 x 10^-12N⁻¹m⁻²C²)

Applications of Electric Flux

To calculate the electric field around a charged particle or conductor
To solve complex problems in electrostatics

Gauss’ law is an essential theorem in physics that is based on electric flux.

Problems and Solutions

Problem 1. Find the flux through a spherical surface of radius a = 0.5 m surrounding a charge of 10 pC.

Solution:

Given,

q = 10 pC = 10 x 10^-12 C = 10^-11 C

φ = q/ε_o = 10^-11 C/8.85 x 10^-12N⁻¹m⁻²C²

or, φ = 1.13 Nm²C^-1

Problem 2. A square surface with a side length of 4.5 mm is located in a uniform electric field with a magnitude of 2200 N/C. The angle between the normal to the surface and the electric field is 30˚. What is the electric flux through the surface?

Solution:

Given,

E = 2200 N/C

l = 4.5 mm = 4.5 x 10^-3 m

A = l² = (4.5 x 10^-3 m)² = 2.03 x 10^-5 m²

θ = 30˚

Therefore,

φ = EA cos θ = 2200 N/C x 2.03 x 10^-5 m² x cos 30˚

or, φ = 0.039 Nm²C^-1