Gravitational Force

What is Gravitational Force?

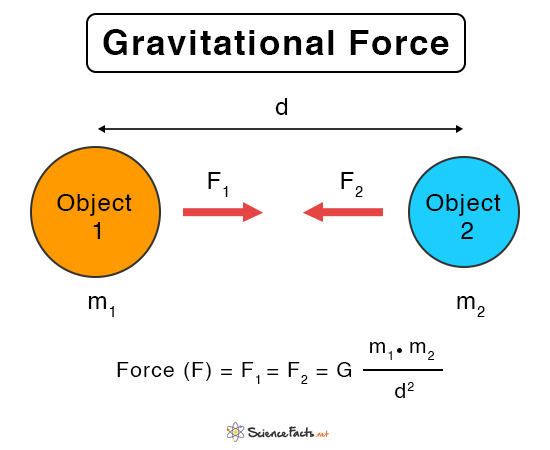
All objects having mass attract each other with force known as the gravitational force. It is quite noticeable in astronomical objects such as Sun, Earth, and Moon that have enormous masses. The reason is that the force is proportional to the products of the objects’ masses. Gravitational force is responsible for keeping the planets in motion around the Sun and the Moon around the Earth. Even human beings exert a force on each other, but it is insignificant because of relatively low masses.

Gravitational force is non-contact since there is no contact between the objects. It is centripetal since it is directed toward the center of the orbit around which the object moves. It is responsible for keeping the body in orbit. The revolving body feels a tug that is directed away from the center. This tug is called the centrifugal force. The gravitational force is the weakest of all fundamental forces.

Many famous scientists have made significant contributions to the field of gravitation. In the early 17th century, Italian astronomer Galileo Galilei found that all objects accelerate equally toward the center of the Earth. English mathematician Isaac Newton was the first to discover the laws of gravitation in his 1687 seminal work.

Universal Laws of Gravitation

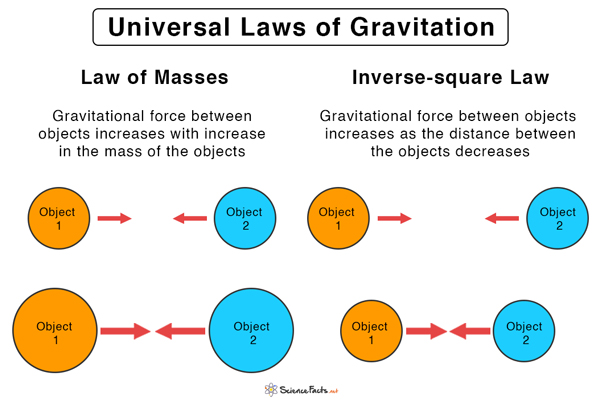
Also known as Newton’s Law of Universal Gravitation, the law states that all objects with a mass in the universe attract each other with a force that is

directly proportional to the product of the masses
inversely proportional to the square of the distance between their centers

These are the two factors that affect the gravitational force. The value is high for massive objects and when the bodies are closer to one another.

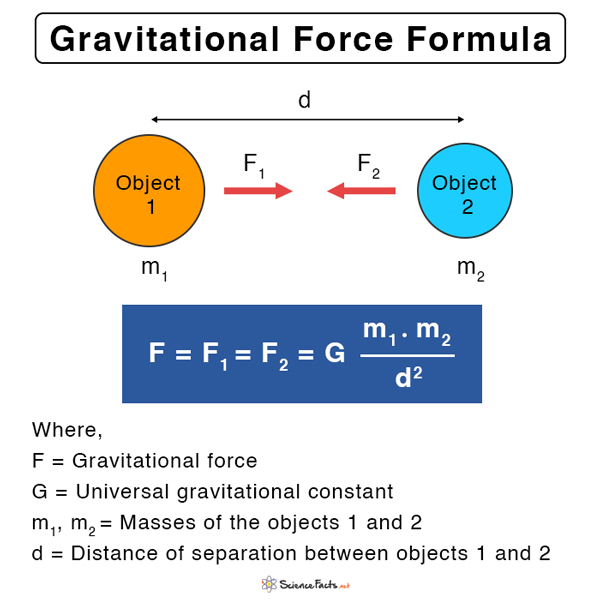
General Formula for Gravitational Force

Suppose M₁ and M₂ be the masses of the two bodies, and R be the distance of separation between their centers. The following equation gives the gravitational force between the two objects.

\[ F = \frac{GM_1M_2}{d^2} \hspace{2 cm} (1) \]

Unit of Gravitational Force: N or Newton

Here, G is called the universal gravitational constant. It is an empirical physical constant with a value of 6.67 X 10^-11N.m²/kg². Its dimensional formula is M^-1L^-3T^-2. By knowing the masses M₁ and M₂ and their distance of separation d, it is possible to calculate the magnitude of F.

Properties of the Gravitational Force

Here are some facts and characteristics of gravitational force.

Attractive
Non-contact
Long-range
It does not require a medium
Directly proportional to the product of the masses of the objects
Inversely proportional to the square of the distance of separation between the objects
A constant value on the surface of the Earth
Weakest of all fundamental forces
Acts along the line joining any two bodies

Examples of Gravitational Force

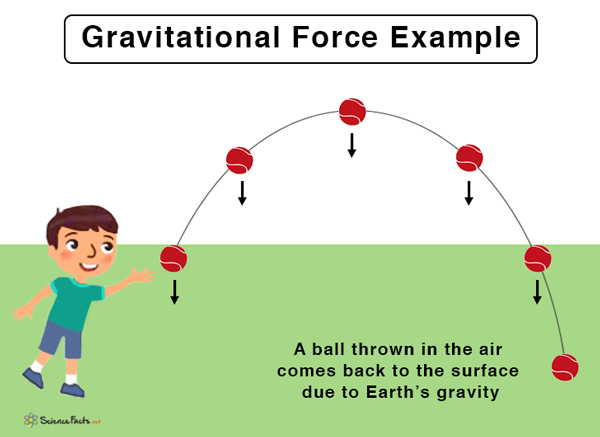
An example of gravitation force in our daily lives is that when an object is thrown in the air, it returns to the surface due to Earth’s gravitation. Below are some more examples.

1. Gravitational Force of the Earth

Earth exerts a gravitational force on every object, a phenomenon known as gravity. Gravity holds us on the surface and does not let us float freely in the air. We exert the same force on Earth that the Earth exerts on us. However, the Earth is so massive that it is unperturbed. An object suspended in air will fall freely towards the center of the Earth when released.

The difference between gravitational force and gravity is that the former is applied to any two objects in the universe. Gravity is the force between Earth and any other object close to Earth, including on its surface.

The force of gravity is given by,

\[ F = \frac{G\hspace{0.1 cm}M_E\hspace{0.1 cm} m}{R_{E}^2} \hspace{2 cm} (2)\]

Where M_E is the mass of the Earth, m is the mass of an object, and R_E is the Earth’s radius. If the object is at an altitude h above the surface of the Earth, then the equation modifies to

\[ F = \frac{G\hspace{0.1 cm}M_E\hspace{0.1 cm} m}{(R_{E}+h)^2} \hspace{2 cm} (3)\]

From the above equation, it is quite clear that the Earth’s gravitational force vanishes when h →∞, or at large distances from the surface.

According to Newton’s second law of motion, force is given by mass m multiplied by acceleration a. Therefore,

\[ F = ma \hspace{2 cm} (4) \]

Comparing equations (2) and (4),

\[ a = g = \frac{G\hspace{0.1 cm}M_E\hspace{0.1 cm}}{R_{E}^2} \hspace{2 cm} (5) \]

The above term is called acceleration due to gravity. It has a value of 9.81 m/s² on the surface of the Earth. Multiplying g by the mass of a person gives the weight W of the person.

\[ W = mg \hspace{2 cm} (6) \]

The acceleration due to gravity in space is zero, which is why astronauts feel weightless and float freely.

The following expression gives the work done by Earth’s gravitational force when an object of mass m falls from a height h above the Earth’s surface.

\[ \text{Work done} = mgh \hspace{2 cm} (7) \]

This work is the change in the object’s potential energy as the object falls through the air.

Satellites orbit around the Earth in fixed orbits due to the gravitational pull. Without gravity, the satellites would have been flung away into space.

The gravity in the polar region is higher than that at the equator. The reason is that the poles are closer to the center of the Earth than the equator.

Gravitational Force Between Earth and Moon

The Moon revolves around the Earth because gravitational forces hold them together. To calculate this force, we put their masses and the distance between their two centers in equation (1).

Mass of the Earth: M_E = 6.0 x 10²⁴ kg

Mass of the Moon: M_M = 7.35 x 10²² kg

The average distance between the Earth and Moon, R_EM = 3.844 x 10⁸ m

Universal gravitational constant, G = 6.67 x 10^-11 Nm²/kg²

From equation (1),

\[ F = \frac{G M_E M_M}{R_{EM}^2} \\ \Rightarrow F = \frac{6.67 \times 10^{-11} \hspace{0.1 cm} N \cdot m^{2} \cdot kg^{-2} \times 6.0 \times 10^{24} \hspace{0.1 cm} kg \times 7.35 \times 10^{22} \hspace{0.1 cm} kg}{ (3.844 \times 10^{8} \hspace{0.1 cm} m)^2} \\ \Rightarrow F = 2 \times 10^{20} \hspace{0.1 cm} N \]

Thus, the gravitational force between the Earth and Moon is 2 x 10²⁰ N.

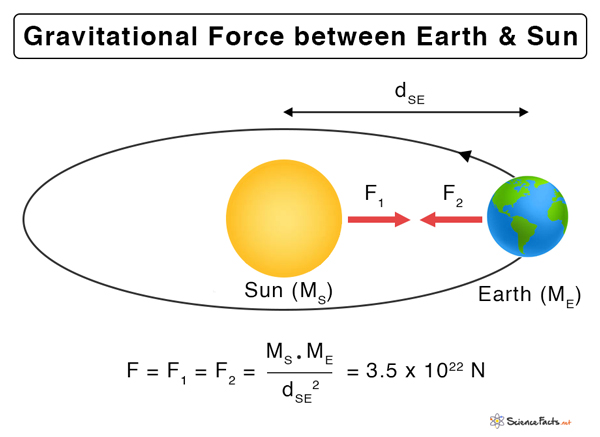
2. Gravitational Force of the Sun

The Sun has a gravitational force due to its mass, which is so large that its influence extends vastly. All planets revolve around the Sun in elliptical orbits due to this attractive force. The gravitational force between the Sun and Earth can be calculated using equation (1).

Mass of the Sun: M_s = 2.0 x 10³⁰ kg

Mass of the Earth: M_E = 6.0 x 10²⁴ kg

The average distance between the Sun and Earth, R_SE = 1.5 x 10¹¹ m

Universal gravitational constant, G = 6.67 x 10^-11 Nm²/kg²

From equation (1),

\[ F = \frac{G M_S M_E}{R_{SE}^2} \\ \Rightarrow F = \frac{6.67 \times 10^{-11} \hspace{0.1 cm} N \cdot m^{2} \cdot kg^{-2} \times 2.0 \times 10^{30} \hspace{0.1 cm} kg \times 6.0 \times 10^{24} \hspace{0.1 cm} kg}{ (1.5 \times 10^{11} \hspace{0.1 cm} m)^2} \\ \Rightarrow F = 3.5 \times 10^{22} \hspace{0.1 cm} N \]

Thus, the gravitational force between the Sun and Earth is 3.5 x 10²² N.

Likewise, the gravitational force between the Sun and other planets will depend upon their masses and distances.

Gravitational Force Between Earth and Sun

3. Gravitational Force of the Planets

All planets of the solar system have their gravitational force. The values of the acceleration due to gravity are given below.

Mercury: 3.7 m/s²
Venus and Uranus: 8.87 m/s²
Mars: 3.71 m/s²
Jupiter: 24.79 m/s²
Saturn: 10.44 m/s²
Neptune: 11.15 m/s²

Besides, the gravity of the Moon is 1.62 m/s². When compared to Earth, it is about 1/6^th.

Advantages and Disadvantages of the Gravitational Force

The gravitational force has significant importance that has impacted our daily lives. Here are some of its benefits.

Constant on the surface of the Earth
It keeps the muscles and bones working
Allows Earth to retain its atmosphere
Allows water dams to store energy

Here are some of its disadvantages.

It makes it difficult to travel to outer space as rockets have to overcome the force of gravity
It makes us fall and get hurt
Limits the height of tall buildings during construction
Hard on the bones and joints as a person ages

FAQs

Q.1. Is gravitational force conservative?

Ans. Yes. The gravitational force is conservative since the work done by it around a close path is zero.

Q.2. Is there gravitational force in a vacuum?

Ans. Yes. There can be a gravitational force in a vacuum.

Q.3. What is the range of gravitational force?

Ans. The range of the gravitational force is infinite, although it becomes weaker as the distance between objects increases.

Q.4. Which measurement changes based on the strength of gravitational force?

Ans. Weight. A person’s weight on Earth is not the same on the Moon due to the difference in gravitational forces.

Q.5. Which force is stronger? Gravitational or electrical?

Ans. The electrical force is stronger than the gravitational force.