Newton’s Second Law

The fundamental characteristic of Newton’s second law is the equation connecting the force, mass, and acceleration. English physicist and mathematician Isaac Newton postulated that acceleration is directly proportional to the force and indirectly proportional to the mass. This hypothesis can be mathematically written as,

a = F/m

Where,

a: Acceleration

F: Force

m: Mass

From the above equation, if the force on the object increases, the acceleration will also increase. On the other hand, if the mass of the object increases while keeping the force constant, the acceleration will decrease. Rearranging the equation,

F = ma

Therefore, the force is equal to the product of mass and acceleration. The above equation is the well-known form of Newton’s second law.

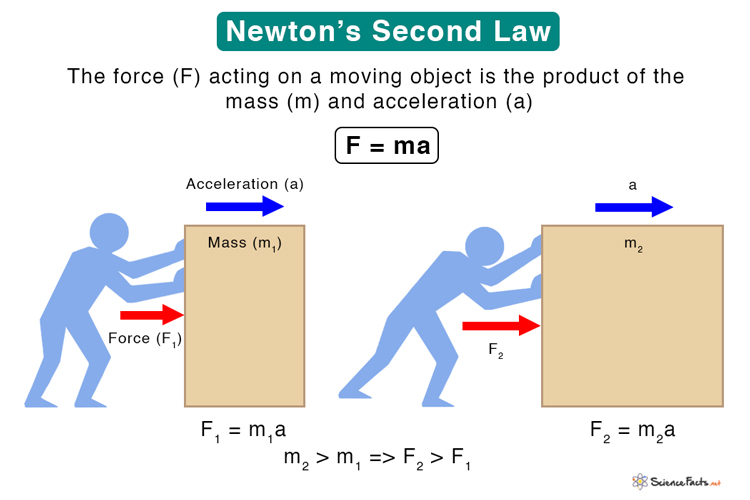
Suppose two objects have masses m₁ and m₂ such that m₁ > m₂. If they are moving with the same acceleration, then the forces F₁ and F₂ acting on them are given by,

F₁ = m₁a

F₂ = m₂a

Since, m₁ > m₂, therefore, F₁ > F₂. It means that a heavy object requires more force than a light object to accelerate by the same amount.

Vector Form

The force equation is written in scalar form. However, force and acceleration are vector quantities. Suppose the object is subjected to many forces, vectorially written as F₁, F₂, F₃…etc. Then, the net force (F) is calculated by vectorially adding all the forces.

F = F₁ + F₂ + F_{3 …}

Or, F = ΣF_n

This force results in an acceleration a in the same direction as the force. Therefore, Newton’s law can be written in vector form as follows,

F = ma

Momentum

The Newton’s second law can be written in terms of momentum (p). Momentum is defined as the product of mass and velocity.

p = m x v

Since acceleration is the change of velocity over time, the force is given by,

F = m(Δv/Δt)

Or, F = Δp/Δt

Where,

Δp: Change in momentum

Δt: Change in time

Therefore, force is defined as the change in momentum over time.

1. Riding a Bicycle

While riding a bicycle, a force is applied on the pedal that makes the bicycle move forward with a specific acceleration. The mass includes the person and the bicycle. The heavier the person, the higher is the force required to move forward.

2. Ball Falling through Air

A ball falls through the air until it hits the surface. The Earth pulls the ball with a force given by the product of the ball’s mass and acceleration due to gravity. This force is equal to the ball’s weight. A heavier ball will experience more force.

3. Rock Rolling Down a Hill

A rock rolls down a hill due to gravity. Its acceleration depends on the inclination of the hill. A heavier rock will roll down with more force.

4. Pushing a Shopping Cart

It is easier to push an empty shopping cart than a filled one. A filled shopping cart has more mass and moves slower when the same force is applied.

5. Launching a Rocket

To launch a rocket into space, it has to overcome Earth’s gravity. A powerful thrust is applied to the rocket. This thrust accelerates the rocket high enough to escape Earth.

6. Driving a Car

The speed of a moving car can be increased by pressing the gas pedal (accelerator). The gas pedal controls the fuel flowing to the engine. Therefore, allowing more fuel to combust the engine provides the car with the power and force necessary to accelerate.

7. Racing Car

A racing car is built such that its mass is low. In this way, the driver can pick up speed and accelerate faster.

8. Hitting a Ball

When a ball is hit with a bat, as in a baseball game, it travels as far as it can. The harder it is hit, the further the distance traveled. The direction of the ball is the same as that of the force.

9. Pushing a Vehicle

When the same force pushes a car and a truck, the truck moves slower as it is heavier than the car.

P.1. How much horizontal force is required to push a 700 kg car with an acceleration of 4 ms²?

Soln.: Given,

m = 700 kg

a = 4 ms^-2

The required force is,

F = 700 kg x 4 ms^-2 = 2800 N

P.2. A force of 15 N acts upon a 4 kg block. Calculate the acceleration of the object.

Soln.: Given,

m = 4 kg

F = 15 N

The acceleration is given by,

a = F/m = 15 N/4 kg = 3.75 ms^-2

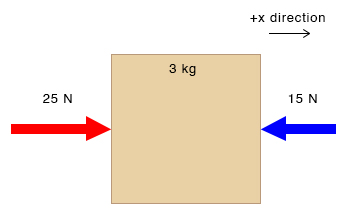
P.3. A block of mass 3 kg is moving on a surface. A force of 25 N acts on it in the positive x-direction and 15 N in the negative x-direction. In which direction is it moving? What is its acceleration?

Soln.: Given,

m = 3 kg

F₁ = 25 N

F₂ = 15 N

Since F₁ > F₂, the object moves in the x-direction.

Net force = F₁ – F₂ = 25 N – 15 N = 10 N

Therefore, the acceleration is,

a = F/m = 10 N/3 kg = 3.33 ms^-2

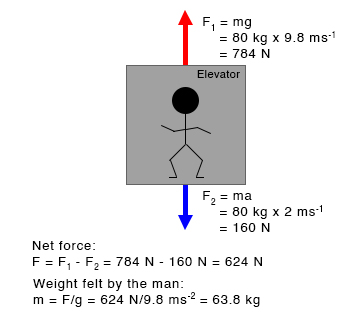
P.4. A man of mass 80 kg on the top floor of a building steps into an elevator. What is the weight felt by the man as the elevator accelerates downward at a rate of 2 ms^-2? (g = 9.8 ms^-2)

Soln: Given,

m = 80 kg

a = 1.5 ms^-2

g = 9.8 ms^-2

According to Newton’s second law, the force is given by,

F = ma

Reaction force on the man by the elevator due to Earth’s gravity:

F₁ = mg = 80 kg x 9.8 ms^-2 = 784 N

Force on the elevator by the man due to acceleration:

F₂ = ma = 80 kg x 2 ms^-2 = 160 N

Since the two forces are opposite each other, the net force is the difference between the two forces.

Net force:

F = F₁ – F₂ = 784 N – 160 N = 624 N

Therefore, the weight felt by the man is,

m = F/g = 624 N/ 9.8 ms^-2 = 63.8 kg

Therefore, a person going down the elevator feels lighter.