Heisenberg Uncertainty Principle

Before the emergence of quantum mechanics, it was widely accepted that it was possible to simultaneously determine all variables of an object with absolute precision at a specific moment. In Newtonian physics, there were no restrictions on the improved methods and techniques developed to reduce the measurement uncertainty potentially. Consequently, imagining that all information could be definitively established with meticulous attention and precision was plausible. However, Heisenberg boldly proposed a fundamental limit to this level of accuracy, inherently introducing uncertainty into our knowledge of a particle.

The Heisenberg Uncertainty Principle has profound implications for quantum mechanics and our understanding of the quantum world. It introduces a level of inherent randomness and unpredictability into the behavior of particles. This uncertainty is not due to limitations in technology but reflects the fundamental nature of particles at the quantum scale.

One of its critical consequences is setting up a fundamental limit to how exactly we can know the state of a quantum system. It has implications for various quantum phenomena, including electron behavior in atoms, the particle properties in quantum fields, and the uncertainty in quantum measurements.

To illustrate Heisenberg Uncertainty Principle, imagine trying to measure the position of an electron with extreme precision. As we narrow down its location, the uncertainty in its momentum increases. Conversely, if we try to determine its momentum with high accuracy, we will lose precision in measuring its position. This inherent uncertainty in measurement at the quantum level challenges our classical notion of determinism, where knowing precisely the initial conditions would enable us to predict future behavior.

When we delve into atomic dimensions, the notion of a particle resembling a solid sphere loses its validity because, as dimensions decrease, particles increasingly exhibit wave-like characteristics. The electron behaving as a wave relates to the quantum mechanical wave function, which is associated with the likelihood of locating the electron in any given spatial location. A perfectly sinusoidal electron wave means momentum is precisely known, diminishing the probability of finding the electron across space.

Let us dive deep into the mathematical formulation of the Heisenberg Uncertainty Principle in quantum physics.

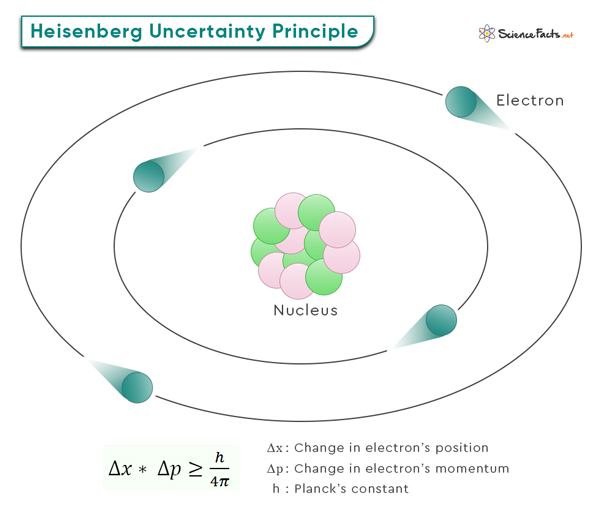
The equation involves two key variables: Δx and Δp. Δx represents the uncertainty in the position of a particle, while Δp signifies the uncertainty in its momentum. Particles do not have definite positions and momenta simultaneously in the quantum world. Instead, they exist in a state of probability. These uncertainties, Δx and Δp, quantify the range of possible values for position and momentum, respectively.

The Heisenberg Uncertainty Principle Equation is often written as

Δx * Δp ≥ h/4π

Where h (= 6.626 x 10^-34 Jˑs) is the Planck’s constant. Another way of writing this equation is

Δx * Δp ≥ ħ/2

Where ħ = h/2π (= 1.055 x 10^-34 Jˑs) is the reduced Planck’s constant.

This equation asserts that the product of the uncertainties in position (Δx) and momentum (Δp) of a particle must always be greater than or equal to a particular constant value. It means that the more precisely we know the particle’s position (Δx becomes smaller), the less accurately we can find its momentum (Δp becomes larger), and vice versa.

Problem 1: Calculate the minimum uncertainty in the velocity of a particle if its position is known within a range of 0.01 nanometers (nm).

Solution:

The Heisenberg Uncertainty Principle is given by:

Δx * Δp ≥ ħ/2

Given Δx = 0.01 nm = 1 x 10^-11 m

Therefore,

Δp ≥ ħ/(2 Δx)

=> Δp ≥ (1.05 x 10^-34 J·s)/(2 x 1 x 10^-11 m)

=> Δp ≥ 5.25 x 10^-24 kg·m/s

So, the minimum uncertainty in the momentum of the particle is approximately 5.25 x 10^-24 kg·m/s

Problem 2: An electron is confined to a region of 0.02 nanometers (nm) in width. Calculate the minimum uncertainty in its velocity and kinetic energy in eV.

Solution:

Using the Heisenberg Uncertainty Principle:

Δx * Δp ≥ ħ/2

But, Δp = m Δv. Therefore,

m Δx * Δv ≥ ħ/2

=> Δv ≥ ħ/(2 m Δx)

Given Δx = 0.02 nm = 2 x 10^-11 m

Mass of the electron (m) = 9.109 x 10^-31 kg

Therefore, 

Δv ≥ (1.055 x 10^-34 J·s)/(2 x 9.109 x 10^-31 kg x 2 x 10^-11 m)

=> Δv ≥  2.88 x 10⁶ m/s

So, the minimum uncertainty in the electron’s velocity is approximately 2.88 x 10⁶ m/s.

The minimum kinetic energy of the particle is

K.E. = ½ m (Δv)²

=> K.E. = ½ x 9.109 x 10^-31 kg x (2.88 x 10⁶ m/s)²

=> K.E. = 3.78 x 10^-18 J = 3.78 x 10^-18 J/1.6 x 10^-19 eV/J = 23.6 eV

So, the minimum uncertainty in the electron’s kinetic energy is approximately 23.6 eV.

Problem 3: An electron in a molecule travels at a 4 x 10⁶ m/s speed. The uncertainty in the momentum Δp of the electron is 0.01 times its momentum. Compute the uncertainty in position Δx if the mass of an electron is 9.1×10⁻³¹ kg using the Heisenberg Uncertainty Formula.

Solution:

The Heisenberg Uncertainty Formula is

Δx * Δp ≥ ħ/2

Given 

Δp/p = 0.01, v = 4 x 10⁶ m/s, and m = 9.1×10⁻³¹ kg

We know

p = m v

Therefore

 Δp = 0.01 x m x v

And

Δx ≥ ħ/(2 x 0.01 x m x v)

=> Δx ≥ 1.055 x 10^-34 J·s /(2 x 0.01 x 9.109 x 10^-31 kg x 4 x 10⁶ m/s)

=> Δx ≥ 1.44 x 10^-9 m/s or 1.44 nm

 So, the minimum uncertainty in the electron’s position is approximately 1.44 nanometers.