Principle of Superposition

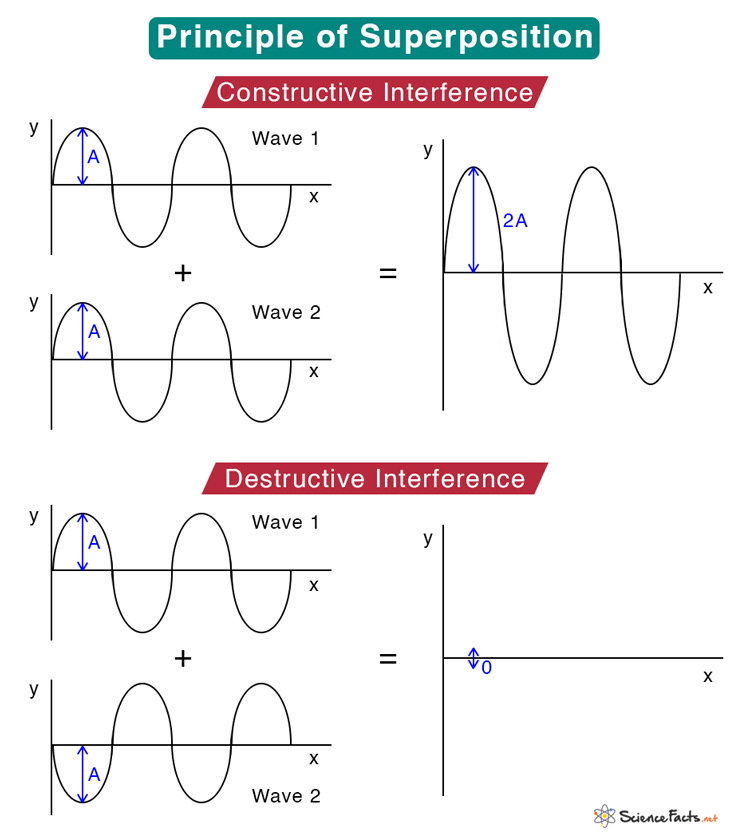
When we talk about disturbances in waves, we refer to the displacement in a vertical plane. Since displacement can be positive or negative, the net displacement can either be greater or less than the individual wave displacements. When both displacements are of the same sign, the resulting interference is called constructive interference. When both displacements have opposite signs, the resulting interference is called destructive interference. Constructive and destructive interferences are illustrated in the image below.

A function F(x) that satisfies the superposition principle is a linear function. In simple mathematical notation, it is written as

 F (x₁ + x₂) = F (x₁) + F (x₂)

Consider two waves whose displacements are given by y₁ and y₂. Then, according to the principle of superposition, the net displacement y is given by

y = y₁ + y₂

The above equation can be generalized to n number of waves whose displacements are y₁, y₂, y₃,…,y_n. In such case, the net displacement is given by

y = y₁ + y₂ + y₃ + … + y_n

For the above equation to be valid, y₁, y₂, y₃, …, y_n must be linear.

Suppose the displacement is a function of the position x. Then, y is written as y ≡ y (x). The superposition of the two functions y₁ (x) and y₂ (x) is given by

y (x) = y₁ (x) + y₂ (x)

Consider a wave traveling along a stretched string with amplitude A, frequency ω, and wave number k. Its time-dependent displacement is given by

y₁ (x, t) = A sin (kω – t)

Another wave traverses along the string but is shifted by a phase ø. Its displacement is given by

y₂ (x, t) = A sin (kω – t + ø)

The two waves are coherent. Let us apply the superposition principle to combine these two waves and obtain the net displacement.

y (x, t) = y₁ (x, t) + y₂ (x, t)

=> y (x, t) = A [sin (kω – t) + sin (kω – t + ø)]

=> y (x, t) = 2A cos (ø/2) · sin (kω – t + ø/2)

Like its constituents, the resultant wave is sinusoidal, traveling in the positive x-direction with an amplitude 2A cos (ø/2). Its phase angle is half the phase difference of its constituent waves.

Problem 1: Two light waves are represented by y₁(t) = 5 sin(ωt) and y₂(t) = 2 sin (ωt + π/2). What will be the resultant amplitude of superposition?

Solution

Given y₁(t) = 5 sin(ωt) and y₂(t) = 2 sin (ωt + π/2) = 2 cos (wt)

The resultant displacement is

y(t) = y₁(t) + y₂(t)

=> y(t) = 5 sin(ωt) + 2 cos (wt)

The resultant amplitude is

A = √(5² + 2²) = 5.39