Stokes’ Law
What is Stokes’ Law
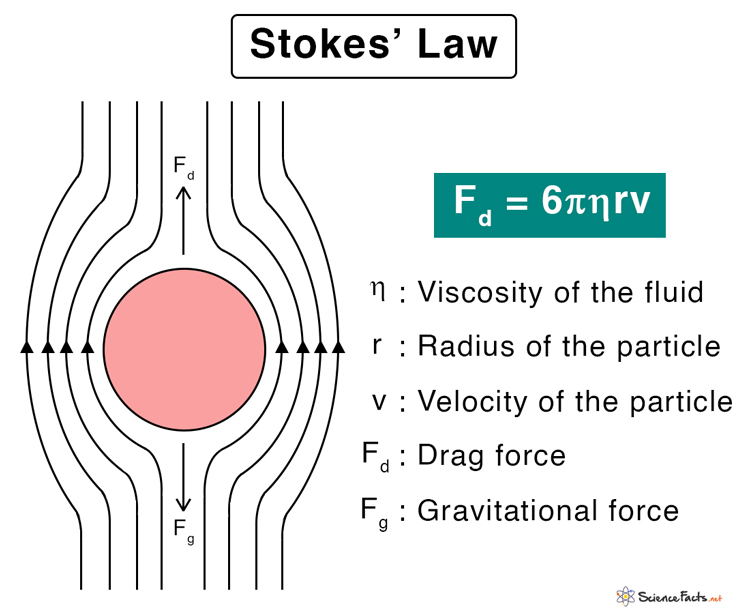
Stokes’ law is a mathematical equation for the drag force experienced by small spherical particles passing through a viscous fluid medium. It deals with the resistive (friction) force applied to a body under the action of gravity as it is dropped into a fluid – liquid or air.
Historically, Stokes’ law has been named after Anglo-Irish physicist and mathematician George Gabriel Stokes after he derived the expression for drag force in 1851.
Stokes’ Law Equation
According to Stokes’ law, the drag force Fd experienced by a spherical particle flowing through a viscous fluid is given by the following formula.
Fd = 6πηrv
Where,
η is the viscosity of the fluid
r is the radius of the particle
v is the velocity of the particle relative to the fluid
SI Unit: Newton or N
Assumption of Stokes’ Law
Stokes’ law is valid under the following conditions.
- Particles must be solid, smooth, and spherical.
- Particles must be of uniform density.
- Particles must be sufficiently large (>0.001mm) as compared to molecules of fluid so that the thermal (Brownian) motion of the fluid molecules does not affect the particles.
- Particles should not interfere with each other during the fall.
- The suspension should not have any turbulence, i.e., the flow must be laminar.
Derivation of Stokes’ Law
Stokes’ law can be derived using dimensional analysis. Consider the forces acting on a spherical particle as it sinks through a liquid column under the action of gravity. The viscous drag force Fd acts on the particle is proportional to the following factors.
- The radius of the sphere, r
- The viscosity of the fluid, η
- The velocity of the particle, v
This proportionality can be represented as,
Fd ∝ ηa rb vc
Replacing the proportionality sign with the equality sign,
Fd = k ηa rb vc
Where k is the dimensionless proportionality constant
Writing the above equation in terms of dimensions,
[MLT-2] = [ML-1T-1]a [L]b [LT-1]c
Or, [MLT-2] = Ma L-a+b+c T-a-c
Equating the superscripts of mass, length, and time on both sides.
1 = a
1 = – a + b + c
– 2 = – a – c
Solving the above set of equations.
a = 1
b = 1
c = 1
Therefore,
Fd = k η r v
Experimentally, the value of k was found to be 6π. Hence,
Fd = 6πηrv
Stokes’ Law and Settling Velocity
Settling or terminal velocity is the maximum velocity attainable by an object as it falls through the fluid. It occurs when the sum of the forces due to drag and buoyancy is equal to the downward force due to gravity. There is no force on the object at the terminal velocity, and hence, the acceleration is zero. The object moves in a steady state.
By using the drag, buoyant, and gravitational forces, the particle’s terminal velocity is given by the following equation,
where,
r is the radius of the particle
ρs is the density of the particle
ρf is the density of the fluid
Applications of Stokes’ Law
Stokes’ law is used in the falling-sphere viscometer, in which a sphere of known density descends a vertical tube. The terminal velocity can be measured by recording the time and the distance traveled. This device is used to measure the viscosity of a fluid.
Sedimentation is the propensity for particles in suspension to settle out of the fluid as deposits known as sediments. Stokes’ law is essential in understanding the sedimentation of small particles under the force of gravity. It can determine the sedimentation rate, which is the sediment’s terminal velocity.
Stokes’ law can explain the floatation of clouds. Since raindrops are smaller in size, their terminal velocities are small. Therefore, they remain suspended in the air in the form of clouds. As they increase their size, their terminal velocities increase, and they start falling in the form of rain.
When jumping off a plane, a parachute helps a person to slow down and land softly. The reason is that the person with the parachute achieves a terminal velocity.
In Millikan’s oil drop experiment, Stokes’ law is used to determine the electron’s charge.
Limitations of Stokes’ Law
- Some colloidal particles of the same mass fall slower than others due to the difference in the shapes of particles.
- Many fast-falling particles may drag finer particles down along with them.
- Particles greater than 0.08 mm in diameter settle quickly and cause turbulence
-
References
Article was last reviewed on Thursday, February 2, 2023