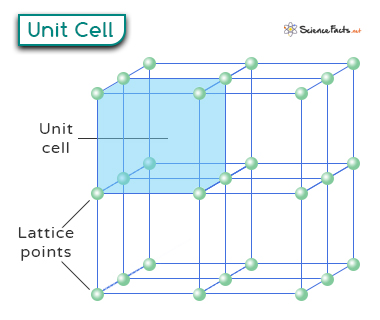
Unit Cell

There are several types of unit cells, each with unique characteristics. Let us take a cubic unit cell as an example. A cubic unit cell has all its edges of equal length and all angles between them equal to 90 degrees. There are three main types of cubic unit cells:

1. Simple Cubic Unit Cell: The simple or primitive cubic unit cell has equal sides and angles, making it symmetrical in all directions. Each lattice point is situated at the corners of the cube. The atoms touch along the edges of the cube.
2. Body-Centered Cubic (BCC) Unit Cell: In a body-centered cubic unit cell, one lattice point is at each corner of the cube, similar to the simple cubic unit cell, and an additional lattice point is positioned at the center of the cube. Metals like iron and tungsten often exhibit this type of structure.
3. Face-Centered Cubic (FCC) Unit Cell: In a face-centered cubic unit cell, one lattice point is at each corner of the cube, similar to the simple cubic unit cell, and an additional lattice point is at the center of each face of the cube. The FCC structure is commonly found in metals such as copper and aluminum.

The “number of atoms per unit cell” refers to the count of individual atoms contained within a single unit cell. This value depends on the type of crystal structure and the arrangement of atoms within the unit cell. Let us calculate this number for each of the above three types of cubic unit cells.

1. Simple Cubic Unit Cell

The simplest arrangement of atoms is found in the simple cubic unit cell. Crystallographers focus on the atoms at the corners to calculate the number of atoms in the unit cell. In this case, one-eighth of an atom at each corner contributes to the unit cell. Therefore, the total number of atoms (N) in a simple cubic unit cell is given by N = 1/8 × 8 = 1, resulting in one atom per unit cell.

In addition to the number of atoms per unit cell, crystallographers are also interested in the coordination number. It represents the number of nearest neighbors each atom has. The coordination number of a simple cubic unit cell is relatively low, being 6. It means that each atom in a simple cubic structure is in direct contact with six neighboring atoms.

2. Body-Centered Cubic (BCC) Unit Cell

In the BCC structure, determining the number of atoms involves not only counting those at the corners but also incorporating the central atom. Here, eight atoms are at the corners, each contributing 1/8, and one atom at the center, contributing the full cell. Then, the total number of atoms (N) in a BCC unit cell is given by N = 1/8 × 8 + 1 = 2, resulting in two atoms per unit cell.

The coordination number in a BCC structure is higher than that in a simple cubic structure, with each atom in contact with eight neighboring atoms. This increased coordination number contributes to the enhanced mechanical strength and stability of BCC metals.

3. Face-Centered Cubic (FCC) Unit Cell

In the FCC unit cell, counting atoms involves considering those at the corners and those on the faces. Each of the eight corners contributes 1/8 of an atom, and each of the six faces contributes one-half. The total number of atoms (N) in an FCC unit cell is thus given by N = 1/8 × 8 + 1/2 × 6 = 4, resulting in four atoms per unit cell.

The coordination number in an FCC structure is the highest among the three types, with each atom in contact with 12 neighboring atoms. This close-packed structure contributes to the high symmetry and stability observed in FCC metals and alloys, making them essential in various industrial applications.

The physical properties of crystalline solids are determined by the arrangement and structure of their unit cells. Unit cells are the repeating building blocks that make up a crystal lattice. They play a crucial role in determining various characteristics of crystals, such as their density, melting point, and mechanical properties.

1. Density

The packing efficiency of the unit cells influences the density of crystals. The closer the atoms or ions are packed together within a unit cell, the higher the density of the crystal will be. A more tightly packed structure allows more particles to occupy a given volume.

2. Melting Point

The melting point of crystals is also affected by their unit cell structure. The strength and type of bonding between atoms or ions within a unit cell determine how much energy is required to break those bonds and convert the solid crystal into a liquid state. Crystals with strong intermolecular forces will have higher melting points than those with weaker forces.

3. Mechanical Properties

The mechanical properties of crystals, such as hardness and elasticity, are also determined by their unit cell arrangements. The specific bonding patterns between atoms or ions within a unit cell can influence how easily they can be displaced or deformed under external stress.