Wave-Particle Duality

Several theories have been proposed to explain this intriguing phenomenon. Three important ones are the de Broglie hypothesis, Heisenberg uncertainty principle, and Schrödinger’s wave equation.

1. De Broglie Hypothesis

Proposed by Louis de Broglie in 1924, this hypothesis suggests that all particles, including matter, have wave-like properties. De Broglie proposed that the wavelength of a particle is inversely proportional to its momentum. It means that even macroscopic objects, like baseballs or cars, have an associated wavelength. However, it is tiny and difficult to observe. This idea paved the way for the development of wave-particle duality.

De Broglie proposed that a particle of momentum p would have a wavelength λ given by the equation:

λ = h/p

Where h is the Planck’s constant. This wavelength is known as de Broglie wavelength.

2. Heisenberg Uncertainty Principle

Formulated by Werner Heisenberg in 1927, the uncertainty principle asserts that it is impossible to simultaneously determine the precise position and momentum of a particle with absolute certainty. This principle places a fundamental limit on our ability to measure these properties accurately. It implies that particles do not possess definite positions or momenta until observed, suggesting a wave-like behavior where probability distributions describe the particle’s properties.

The uncertainty principle can be conceptualized in mathematical notation, which states that the product of the uncertainties in position (Δx) and momentum (Δp) cannot be less than Planck’s constant over four pi.

(Δx) (Δp) ≥ h/4π

3. Schrödinger’s Wave Equation

Developed by Erwin Schrödinger in 1926, this equation describes how the wave function of a quantum system evolves over time. The wave function represents the probability distribution of finding a particle at a given position and time. It incorporates wave-like and particle-like characteristics, allowing us to calculate the possible outcomes of experiments involving quantum systems. Schrödinger’s equation provides a powerful tool for understanding and predicting the behavior of particles on a quantum level.

Having explored the theories explaining wave-particle duality, let us explore real-world examples demonstrating this intriguing phenomenon and understanding the fascinating duality of matter. Here are three well-known examples.

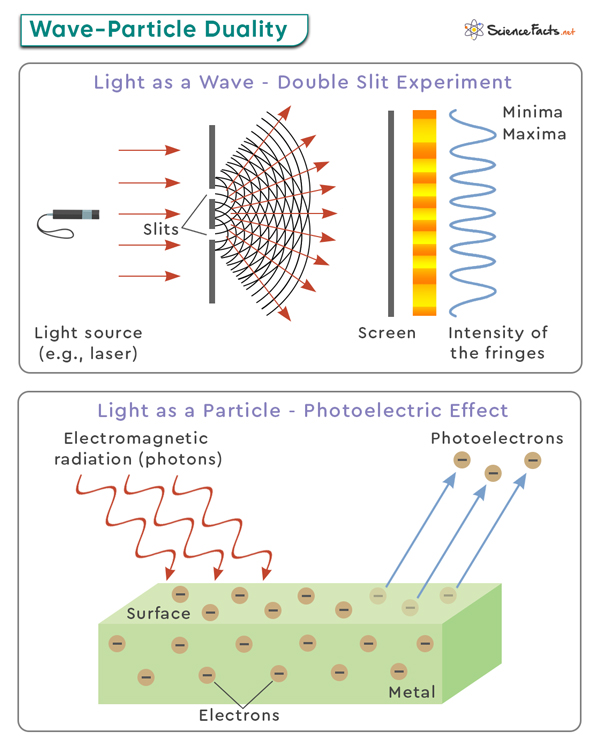
1. Young’s Double-slit Experiment

In this experiment, a beam of light is sent through two closely spaced slits and observed on a screen behind them. When the light passes through the slits, it creates an interference pattern on the screen, similar to what would be expected from waves. However, when the experiment is repeated with individual particles, such as electrons or even larger molecules, they also create an interference pattern, suggesting that these particles can behave like waves.

2. Photoelectric Effect 

The photoelectric effect occurs when light shines on a metal surface and causes the emission of electrons. According to classical wave theory, light intensity should determine the energy of emitted electrons. However, experiments revealed that only light above a specific frequency (threshold frequency) causes electron emission, regardless of intensity. This observation concluded that light can act as discrete packets of energy called photons, exhibiting particle-like behavior.

We can analyze the photoelectric effect by using the energy conservation law. The total energy of the incoming photon must be equal to the kinetic energy of the ejected electron plus the energy required to eject the electron from the metal, which is described mathematically by the photoelectric equation:

E = φ + KE

Where:

E represents the energy carried by a single photon of light of frequency ν (E = hν).

KE represents an electron’s kinetic energy after being emitted from the material. 

φ is the work function and refers to the minimum energy required to remove an electron from a specific material. 

3. Davisson-Germer Experiment 

In this experiment, a beam of electrons was directed at a crystal surface and observed for scattering patterns. The scattered electrons were expected to behave like particles bouncing off the crystal lattice. Surprisingly, the results showed a diffraction pattern similar to what is expected from waves passing through a double slit. This experiment demonstrated that electrons can exhibit wave-like behavior, supporting the idea of wave-particle duality.

These examples highlight how various experiments have shown that particles like photons and electrons can exhibit wave-like and particle-like properties depending on their interactions. Wave-particle duality challenges our intuitive understanding of matter, which is now a central concept in modern physics.