Angular Momentum

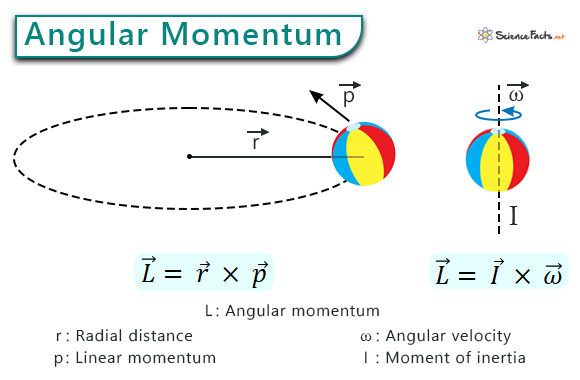
In linear dynamics, the product of mass and velocity gives linear momentum. In rotational dynamics, the angular momentum of a point object is defined as the product of the linear momentum and the perpendicular distance from the axis of rotation. For a stationary spinning object, angular momentum is defined as the product of the moment of inertia and angular velocity. It is a vector quantity and has both magnitude and direction.

Any rotating or spinning object with mass has angular momentum. For example, the Earth has orbital angular momentum as it rotates about the Sun while completing a year and spin angular momentum as it spins about its axis while completing a day.

Formula

Suppose p is the linear momentum and r is the object’s perpendicular distance from its rotation axis. The angular momentum (L) is

L ꓿ rp

The above equation is the general way of writing the magnitude of the momentum. Specifically, it applies to a point object rotating about a fixed point. In vectorial notation, the angular momentum is given by

\[ \vec{L} = \vec{r} \times \vec{p} \]

We can expand the cross-product by introducing θ as the angle between \( \vec{r} \) and \( \vec{p} \).

L ꓿ r p sin θ

The term r sin θ is the perpendicular distance from the point object to the axis and can be written as r_⊥.

L = r_⊥p

Angular Momentum and Moment of Inertia

So far, we have talked about a point mass rotating about a fixed point. We can expand this concept of angular momentum to extended spinning objects. The linear momentum is given by the product of the mass (m) and linear velocity (v). The angular momentum becomes

L ꓿ mvr

Any rotating object has an angular velocity (ω) related to the linear velocity.

v ꓿ ωr

Therefore,

L ꓿ mωr²

However, mr² is the moment of inertia (I) of a point mass rotating about an axis at a distance r.

I ꓿ mr²

Therefore,

L ꓿ Iω

The above equation applies to any rigid rotating object. The moment of inertia values can be found in standard tables for well-defined objects.

In vectorial notation, the above equation is given by

\[ \vec{L} = I\vec{\omega} \]

When the rotation is aligned with the rotating object’s principal axes, the direction of the angular momentum vector is along the axis of rotation of the given object. The righthand rule can best describe it. If the fingers curl along the direction of rotation, the thumb points toward the angular momentum.

Unit and Dimension

The SI unit of angular momentum is kg·m²/s. Its dimensional formula is [M L² T^─1].

Example Problems

Problem 1. Calculate the angular momentum of a pulley whose mass is 1 kg, the radius is 0.05 m and rotates at a constant angular velocity of 6 rad/sec.

Solution

Given

m ꓿ 1 kg, r ꓿ 0.05 m, and ω ꓿ 6 rad/s

The angular momentum is

L ꓿ Iω

The moment of inertia of a pully is

I ꓿ ½ mr² ꓿ ½ x 1 kg x 0.05² m²꓿ 0.00125 kg·m²

Therefore,

L ꓿ 0.00125 kg·m² x 6 rad/s ꓿ 0.0075 kg·m²/s

Problem 2. A spacecraft of mass = 2500 kg orbits a planet in a circular path with a radius = 5.7 x 10⁶ m. The spacecraft has a linear velocity = 9.1 x 10³ m/s. Calculate the angular momentum of the spacecraft.

Solution

Given m = 2,500 kg, r = 5.7 x 10⁶ m, and v = 9.1 x 10³ m/s

The angular momentum of a point object is

L = mvr

=> L = 2500 kg x 9.1 x 10³ m/s x 5.7 x 10⁶ m = 1.3 x 10¹⁴kg·m²/s