Angular Velocity
When an object rotates or revolves, it sweeps out an angle about an axis or a point. The difference between the initial and the final angular positions gives the angular displacement. The angular velocity is the rate at which the angular displacement changes. It tells us how fast the object is rotating about its axis or revolving around a fixed point. For instance, a spinning top has angular velocity.
Angular velocity is also known as rotational velocity. It is a vector quantity, which means it has both magnitude and direction.
Types of Angular Velocity
There are two types of angular velocity:
Orbital angular velocity refers to how fast an object revolves around a fixed point, typically taken as the origin. Therefore, it is the time rate of change of its angular displacement relative to the origin. For example, the Earth revolves around the Sun. It has an orbital angular velocity.
Spin angular velocity refers to how fast a rigid body rotates about an axis, irrespective of the choice of origin. For example, a bicycle wheel rotates about its axis. It has a spin angular velocity.
Formula
The Greek symbol omega or ω represents the angular velocity. Mathematically, it is the time rate of change of angular displacement θ.
Units and Dimensions
The SI unit of angular velocity is radians per second or radˑs-1. Another unit is revolutions per minute or RPM. The conversion between degrees, radians, and revolutions is quite simple.
1 revolution = 3600 = 2π radians
and, 1 RPM = 0.10472 rad/s
The dimensional formula is [M0 L0 T-1].
Direction
The right-hand rule conventionally specifies the direction of angular velocity. According to this rule, if the fingers curl in the direction of rotation, the thumb points toward the angular velocity. For a revolving object, the angular velocity direction is always perpendicular to the plane of revolution.
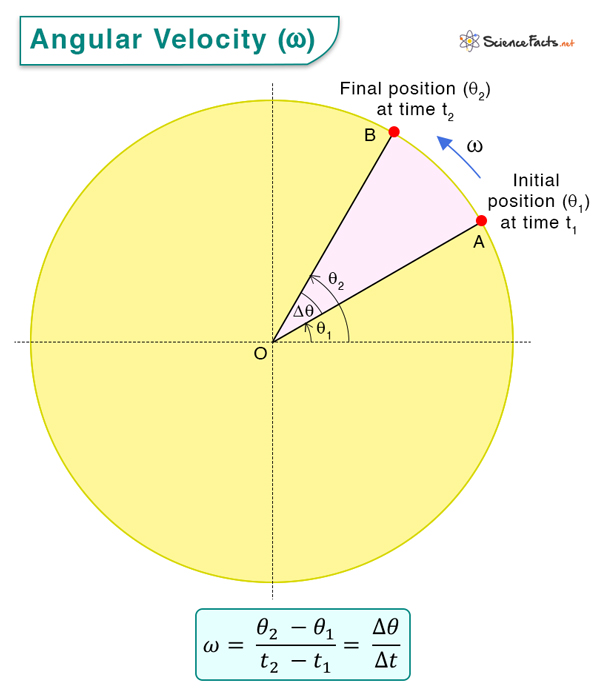
Average and Instantaneous Velocity
The above expression is the formula for the average angular velocity. It considers the angular displacement between any two positions and the time taken by the object to move between those two positions. It can also be conveniently written as
Where θ1 and θ2 are the object’s initial and final angular positions, respectively, and t1 and t2 are the times the object was at these positions.
We can also define instantaneous velocity, which is the instantaneous rate of change of angular displacement. It is obtained by taking the limit of the average angular velocity as the time interval (Δt) approaches zero. Mathematically, it is the time derivative of the angular displacement.
Relation Between Linear and Angular Velocity
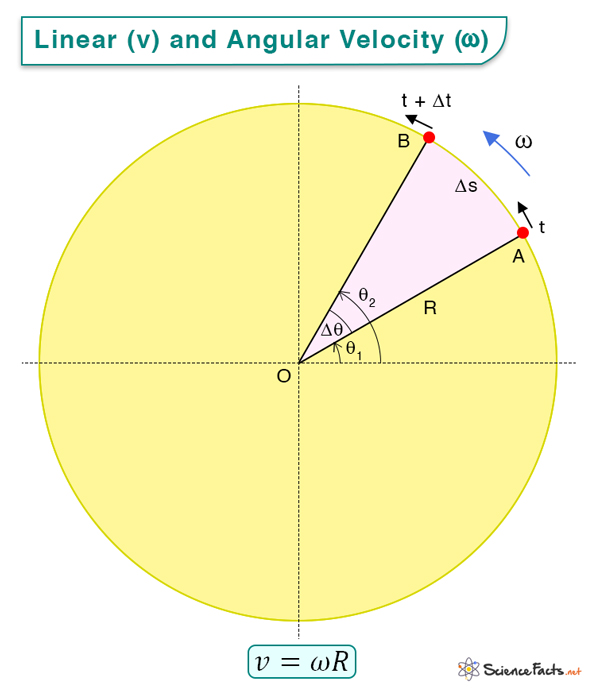
In translational motion, the linear velocity tells us how fast the object moves in a straight line. The angular velocity tells us how fast the object rotates. It is analogous to linear velocity. The two quantities are related. Let us take an example of a rotating disc.
A disc of radius R rotates counterclockwise about an origin O, as shown below. Consider an arc AB = Δs on its rim such that, in the triangle OAB,
The linear velocity v of the disc is always tangential to the points A and B and is given by
Therefore, linear velocity is the product of the angular velocity and the radial distance or radius.
The angular velocity does not change with radius, but linear velocity does. When an object rotates about an axis, every point on the object has the same angular velocity. However, points farther from the axis move at a greater linear velocity than points closer to it.
Angular Velocity of the Earth
The angular velocity plays a crucial role in understanding rotational motion, from celestial bodies to spinning objects in everyday life. The Earth rotates about its axis, completing one rotation every 24 hours. Earth’s angular velocity can be calculated as follows:
1 rotation = 2π radians and 1 hour = 3600 s
Therefore,
Example Problems
Problem 1. Calculate the angular velocity of a 40 cm radius car tire when the car travels at 40 km/h.
Solution
Given R = 40 cm = 0.4 m and v = 40 km/h = 40 x 103 m/(1 x 3600 s) = 11.11 m/s
Therefore, the angular velocity is
ω = v/R = 11.11 mˑs-1/0.4 m = 27.8 radˑs-1
Problem 2. How many revolutions does a turntable make if it moves at 36 rad/s and for 6 minutes?
Solution
Given ω = 36 rad/s and Δt = 6 min = 360 s
The turntable has been rotated by
Δθ = ωΔt = 36 rad/s x 360 s = 12960 rad
We know that
2π rad = 1 revolution
Therefore,
12960 rad = 1 revolution/2π rad x 12960 rad = 2062 revolutions
-
References
Article was last reviewed on Friday, June 30, 2023