Atomic Orbital
What Is An Atomic Orbital?
From the electron cloud model concept, we already know that electrons do not revolve around the atomic nucleus in fixed orbits. Instead, they form a cloud of negative charge around the nucleus. This concept was given by Schrödinger through an equation called the Schrödinger equation.
By solving the equation, we obtain a mathematical expression, called wave function, which describe the probability of finding electrons at certain regions within an atom. This wave function can be described as atomic orbital.
In simple words, atomic orbital refers to a region of space with a high probability of finding the electron. It is depicted as a three-dimensional region with a 95% probability of tracing an electron. On the contrary, the regions around the atomic nuclei where the likelihood of finding electrons is zero are referred to as nodes or nodal planes.
Types of Orbitals
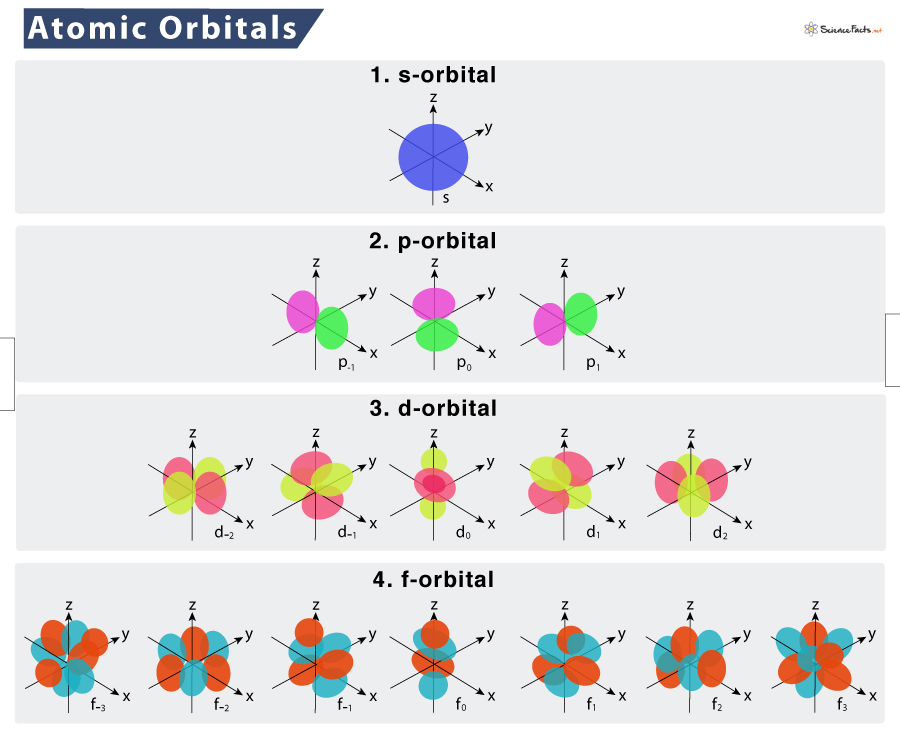
Atomic orbitals are of four different types: s, p, d, and f. They are commonly denoted by a combination of letters and numerals, such as 1s, 2p, 3d, 4f, etc. Here, the numerals indicate principal quantum numbers (n), designating the energy levels as well as relative distance from the nucleus. On the other hand, the letters s, p, d, and f denote the orbital shape.
Each orbital can only accommodate two electrons due to their spin. As the energy levels increase, the electrons are located further from the nucleus, making the orbitals bigger. The number of orbitals that each subshell can accommodate depends on the values of magnetic quantum number (ml). The value of ml ranges from -ℓ to +ℓ, including zero, where ‘ℓ’ stands for azimuthal quantum number.
s orbital
It is a spherical space encircling the nucleus. As it is spherically symmetrical, there is an equal probability of finding electrons in all directions. The size of the orbital increases with the increase in principal quantum number (n). The order of size is 1s < 2s < 3s < 4s and so on. We get a single ‘ml’ value for s-orbital, i.e., zero. So, every subshell has only one s-orbital.
p orbital
As we move from the first energy level, there is another orbital called p orbital. It looks like two lobes or ballons tied at the nucleus, giving a dumbbell shape. Electrons can be found in either of the two lobes. The ‘ml’ value for p orbital ranges from -1 to +1, i.e., -1, 0, +1 (here, ℓ = 1). Thus, every subshell can accommodate three p-orbital.
Depending on how the lobes lie along the x, y, or z-axis, they are designated as 2px, 2py, and 2pz. The axes of these three p orbitals are mutually perpendicular. Similar to s orbitals, the size of p orbitals increases with an increase in the principal quantum number, such as 2p < 3p < 4p and so on.
d orbital
At the third level, there is another orbital called d orbital, in addition to s and p orbitals. There are five d-orbitals in each subshell, as its ‘ml’ values are -2,-1, 0, +1, +2. These orbitals are designated as dxy, dyz, dxz, dx2–y 2 , and dz2.
Out of these five d orbitals, the first four are clover-shaped. However, the energy of all five d orbitals is the same. Similar to other orbitals, the size of this orbital also increases with an increase in the principal quantum number, such as 3d < 4d < 5d and so on.
f orbital
Upon reaching the fourth energy level, there is f orbital. They are oriented in the shape of double dumbbells. The ‘ml’ value for this orbital ranges from -3 to +3, i.e., -3, -2, -1, 0, +1, +2, +3 (here, ℓ = 3). Thus, every subshell can accommodate seven f-orbital. The size of f orbital can be arranged as 4f < 5f < 6f and so on.
Filling Order of Atomic Orbitals
Electrons enter into each orbital following the Aufbau principle. According to this principle, the subshells get filled in order of increasing value of ‘n + ℓ’. In the case of an equal value of ‘n + ℓ’, electrons are assigned to the subshell having a lower ‘n’ value.
The table below shows the ‘n + ℓ’ value of some orbitals, arranged in increasing order of ‘n’ values:
| Orbital | Principle quantum number (n) | Azimuthal quantum number (l) | Sum (n + ℓ’) |
|---|---|---|---|
| 1s | 1 | 0 | 1 |
| 2s | 2 | 0 | 2 |
| 2p | 2 | 1 | 3 |
| 3s | 3 | 0 | 3 |
| 3p | 3 | 1 | 4 |
| 4s | 4 | 0 | 4 |
| 3d | 3 | 2 | 5 |
| 4p | 4 | 1 | 5 |
| 5s | 5 | 0 | 5 |
| 4d | 4 | 2 | 6 |
| 5p | 5 | 1 | 6 |
| 6s | 6 | 0 | 6 |
| 4f | 4 | 3 | 7 |
| … | … | … | … |
-
References
Article was last reviewed on Thursday, February 2, 2023

Nice ideas