Gravitational Potential Energy

Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field. When the object moves from one position to another, its gravitational potential energy change equals the work done in moving the object.

Gravitational potential energy is also associated with the Earth, which we know as gravity. An object at a specific height above the Earth’s surface possesses gravitational potential energy. When the object is released, its potential energy is converted into kinetic energy. The sum of the two always remains constant because of the conservation of energy law.

Gravitational potential energy helps us to understand the motion of planets. When scientists send spacecraft to other planets, they can precisely calculate how much energy is needed to fuel them.

English mathematician and physicist Isaac Newton published his comprehensive theory of gravitation in 1687.

Examples

A car on top of a hill
A roller coaster at its highest point
A child on top of a slide
The water behind a dam wall
An apple in a tree
A book on a table
A pendulum at its extreme ends
Flower pots hanging off of the deck

Formula

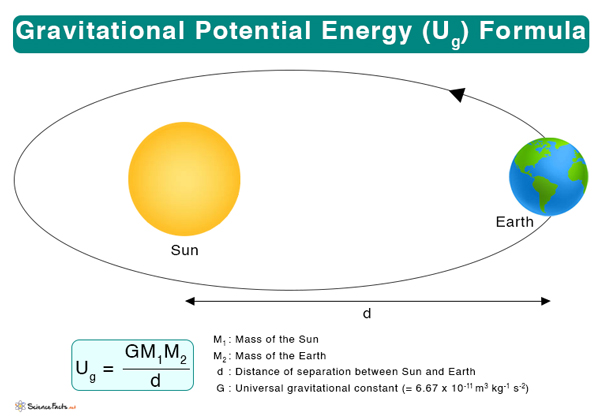
The general equation for gravitational potential energy comes from the universal law of gravitation. According to this law, every object possesses gravitational force due to its mass. Consider two massive objects in space. Let us call them source and test objects. The energy stored by the test object when brought from infinity to a point inside a gravitational field is

\[ U_g = – \frac{GM_1 M_2}{d} \]

Where

U_g: Gravitational potential energy

M₁: Mass of the source object

M₂: Mass of the test object

d: Distance of separation between the two objects

G: Universal gravitational constant (= 6.67 x 10^-11m³ kg^-1 s^-2)

Symbol: U_g

SI Unit: Joules

Dimension: [ML²T^-2]

Why is Gravitational Potential Energy Negative

The gravitational force does positive work in bringing the test object from infinity to a point inside the gravitational field. Because of its inverse square nature, the gravitational force is zero at infinity. Therefore, infinity is taken as the reference point. Moreover, the source object binds the test object to an orbit. This “bound state” results in negative potential energy, as seen in the equation.

Earth’s Gravitational Potential Energy

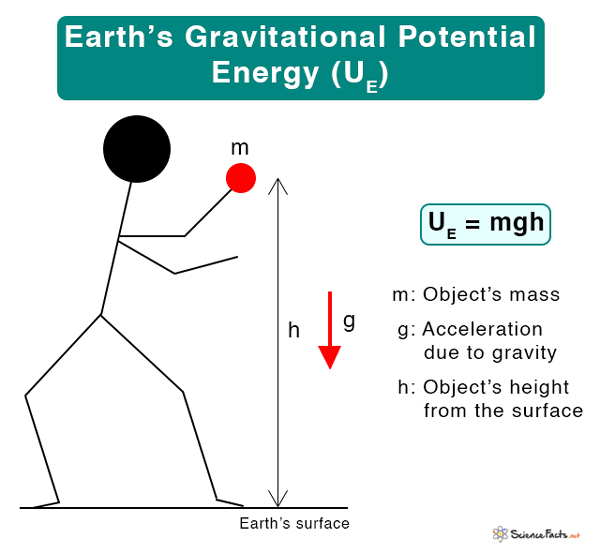
The Earth has a gravitational force which we all know as the force due to gravity. The acceleration due to gravity can be considered to be approximately constant. The expression for the gravitational potential energy of an object relative to the Earth’s surface is

\[ U_E = mgh \]

Where

U_E: Gravitational potential energy due to Earth

m: Mass of the object

h: Height of the object above the Earth’s surface

g: Acceleration due to gravity (=9.81 m/s²)

From the above equation, it is clear that the gravitational potential energy due to Earth depends upon two factors – the object’s mass and height. The heavier the object, the greater the energy. Similarly, the higher the object, the higher its potential energy.

When the object is raised from the ground to a height h, the change is gravitation potential energy is

\[ \Delta U_E = U_{final} – U_{initial} = mgh – 0 \]

This change is equal to the work done in lifting the object.

Derivation

We know that the work done is force times displacement. The infinitesimal work dW done to move the test object by a distance dx is given by

\[ dW = F_g dx \]

Where F_gis the gravitational force. At a distance x from the source object, it is given by

\[ F_g = \frac{GM_1M_2}{x^2} \]

Replacing F_g in the dW equation

\[ dW = \frac{GM_1M_2}{x^2} dx \]

Integrating the above from infinity to d

\[ W = \int^d_\infty dW = \int^d_\infty \frac{GM_1M_2}{x^2} dx \\ \Rightarrow W = -\frac{GM_1M_2}{d} \]

Since the work done is the change in gravitational potential energy, we have

\[ W = \Delta U_g = U_{final} – U_{initial} \\ \Rightarrow -\frac{GM_1M_2}{d} = U_g – 0 \\ \Rightarrow U_g = -\frac{GM_1M_2}{d} \]

Gravitational Potential

The amount of energy required to move a unit mass from infinity to a point inside the influence of a gravitational field due to a source mass M. It is given by the following expression.

\[ V_g = -\frac{GM}{d} \]

References
- 1. Gravitational Potential Energy – Hyperphysics.phy-astr.gsu.edu
  2. What is gravitational potential energy? – Khanacademy.org
  3. Potential Energy – Physicsclassroom.com
  4. Gravitational Potential Energy – Farside.ph.utexas.edu
  5. Gravitational Potential Energy and Total Energy – Courses.lumenlearning.com
  6. Gravitational Potential Energy – Phys.libretexts.org
  7. Gravitational Potential Energy – Iu.pressbooks.pub