Normal Force
What is the Normal Force
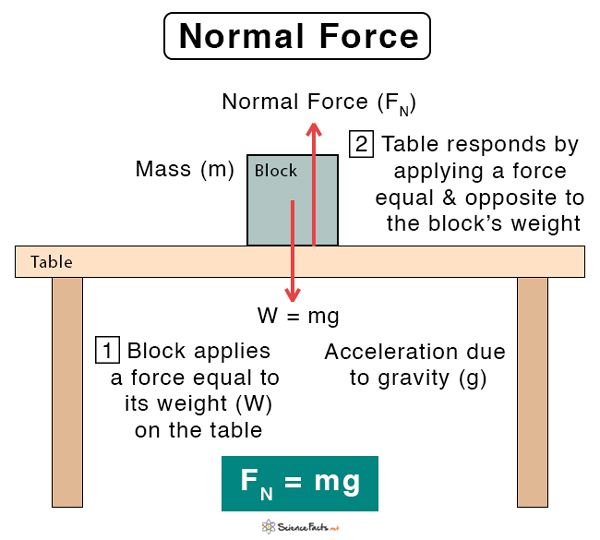
Suppose an object is lying on a surface. It applies a force due to its weight. According to Newton’s third law of motion, the surface responds by applying an equal and opposite force on the object. The component of this force that is perpendicular to the surface is called the normal force. Since the object remains in contact with the surface, the normal force is a contact force.
The normal force balances the weight of the object. However, if other forces act on the body to displace it, friction comes into play. According to the laws of friction, the frictional force is proportional to the normal force.
Examples of Normal Force
There are many examples of normal force, most of which take place in daily life. These include the force applied by:
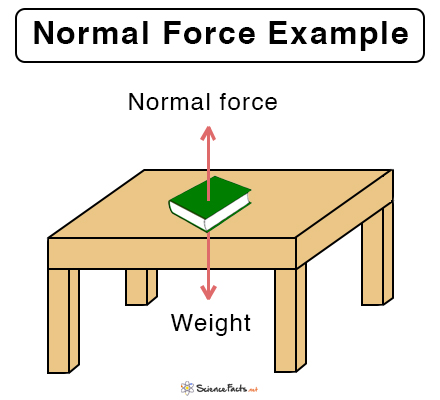
- A table on a book lying on top of it
- A wedge on a block lying on its inclined surface
- Earth upon us
- Human hand while holding an object
- A nail on a hammer during hammering
Characteristics of Normal Force
Here are some facts and properties of the normal force.
- Contact force
- Reaction force
- Perpendicular to the surface
- Opposite to the component of the object’s weight that is perpendicular to the surface
How to Calculate Normal Force
The normal force can be calculated using physics principles and balancing the forces using Newton’s laws of motion.
Normal Force Equations
1. On a Horizontal Surface
Suppose a block of mass m is lying on a horizontal surface. Its weight W is mg, and no other forces are applied to it. The table will apply a force FN on the object. According to Newton’s third law of motion, the normal force is equal to the object’s weight. Therefore, the magnitude of FN is given by,
FN = mg
Symbol of normal force: F
Unit of normal force: Newton or N
Dimensions of normal force: MLT-2
The work done by a force is defined as the force times the displacement.
W = F x d
Since the normal force does not displace the object, so the work done is zero.
W = FN x 0 = 0
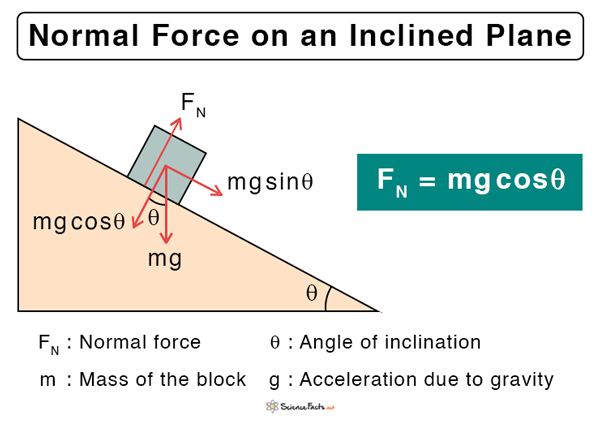
2. On an Incline or Ramp
Suppose a block lies on an inclined plane that makes an angle θ with the horizontal. Its weight mg can be resolved into two components – one parallel to the surface and the other perpendicular to the surface.
The perpendicular component is given by mg cos θ. According to Newton’s third law, this force is equal to the normal force.
FN = mg cos θ
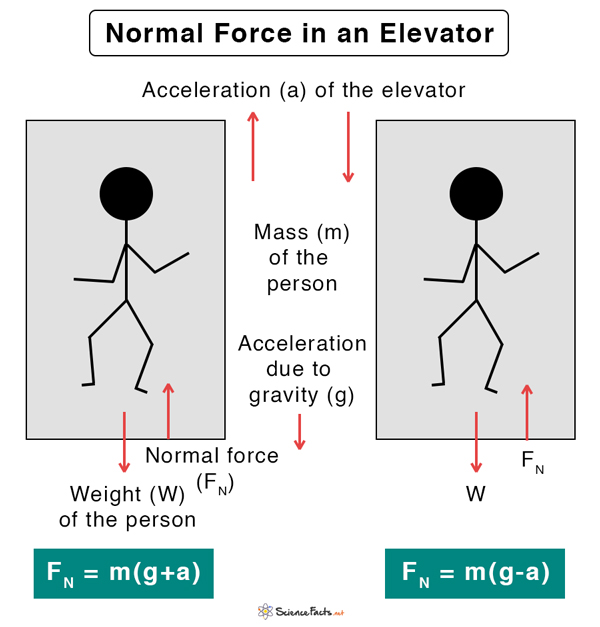
3. In an Elevator
Suppose a person of mass m is inside an elevator which is moving upward with an acceleration a. As the person is in contact with the elevator, he experiences an applied force given by,
FA = ma
Aside, the elevator also exerts a force equal to the person’s weight mg. Therefore, the total force exerted by the elevator on the person is the normal force, which is given by
FN = mg + FA
Or, FN = m(g + a)
In this situation, the normal force is greater than the weight of the person.
Suppose the elevator is moving downwards with the same acceleration, then the force experienced by the person is,
FN = m(g – a)
In this situation, the normal force is less than the weight of the person.
Now, suppose the elevator cable snaps. Then, the elevator moves downwards with an acceleration g, and the force experienced by the person is,
FN = m(g – g) = 0
Therefore, the normal force is zero, meaning that the person is not in contact with the elevator floor. This phenomenon is known as a free fall, and the person feels weightless.
-
References
Article was last reviewed on Friday, February 17, 2023








Your explanation is just WRONG. Please understand Newton’s Third Law before spewing your ignorance around, confusing others, because they take you as an authority:
“…It applies a force due to its weight. According to Newton’s third law of motion, the surface responds by applying an equal and opposite force on the object. ”
No! In your example, Newton’s 3rd law refers to the earth gravitationally attracting the object (action) and the object gravitationally attracting the earch (reaction). You are confusing Newton’s 3rd law with a “statics” problem in which the Normal force counteracts the gravitational force so that the net vertical force acting on the object is zero. Action-reaction pairs must always be the same kind of force. That clearly doesn’t apply here since the Normal force is a contact force and gravitational attraction is not.
You are publishing what is probably the Number One misconception about Newton’s third law made by beginning physics students. So you’re making that misconception worse.