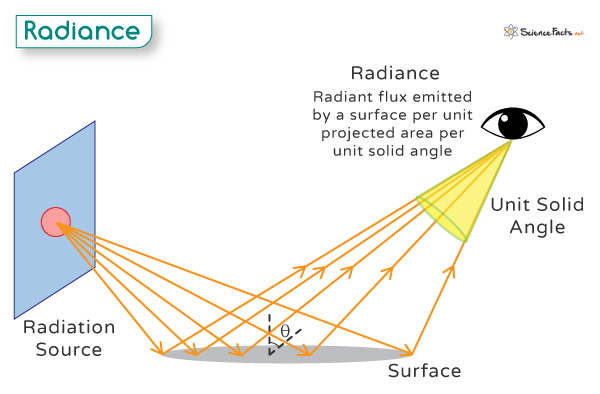
Radiance

Radiance refers to the amount of radiant energy emitted, transmitted, or reflected by a surface or object per second, per unit solid angle, and per unit projected area. It measures how much light travels in a specific direction from a surface. It is like describing the brightness of light not just from one spot but considering both the size of the area it is coming from and its direction.

Simply put, radiance measures how much light comes from a specific area in a specific direction. It tells us how intense the light is when we look at a tiny piece of a surface from a particular angle. For example, when you hold a leaf, the amount of sunlight (brightness) you see coming through the leaf in a specific direction is like measuring the radiance.

Formula

The formula for calculating radiance involves two key parameters: radiant intensity and projected solid angle. Radiant intensity represents the power emitted or reflected by a point source within a specific solid angle. The projected solid angle refers to the area over which this radiant flux is distributed.

The formula for radiance is given by:

\[ L = \frac{\Phi}{A \cdot \omega \cdot \cos(\theta)} \]

Where:

– L is the radiance

– φ is the radiant flux

– A is the area of the source

– ω is the solid angle

– θ is the angle between the surface normal and the radiance direction

This formula accounts for the fact that radiance varies with the angle of observation, with the cosine term (cos θ) representing the geometric relationship between the surface normal and the direction of observation.

Units

Radiance represents the radiant flux per unit area and per unit solid angle. The units of radiant flux, area, and solid angles are Watt (W), meter squared (m²), and steradian (sr), respectively. Therefore, the unit of radiance is watts per meter squared per steradian or W/(m²ˑsr).

Applications

Astronomy: By analyzing the electromagnetic radiation emitted by celestial bodies, astronomers can gain insights into their composition, temperature, and other physical properties.
Remote Sensing: Measuring and interpreting the radiance received from the Earth’s surface or atmosphere enables scientists to gather information about land cover, vegetation health, atmospheric conditions, and other related phenomena. This data is invaluable for environmental monitoring, urban planning, agriculture management, and disaster response.

Example Problems with Solutions

Problem 1: A surface has a radiant flux of 500 W. Calculate the radiance of the surface if the surface area is 2 m² and the solid angle is π steradians. Assume cos θ = 1/π.

\[ L = \frac{\Phi}{A \cdot \omega \cdot \cos(\theta)} \]

Solution:

Given:

Radiant flux: φ= 500 W
Surface area: A = 2 m²
Solid angle: ω = π sr
cos θ = 1/π

Therefore,

$L = 500$

$=> L = 5002 = 250$

The radiance is 250 W/m² ∙ sr

Problem 2: A surface has a radiance of 150 W/(m²·sr) with a solid angle of 0.5 steradian and a surface area of 3 m². Calculate the radiant flux. Assume cos θ = 1/π.

Solution:

$L = d Φ dA \cdot dω \cdot \cos (θ)$