Simple Pendulum

A pendulum is a device that is found in wall clocks. It consists of a weight (bob) suspended from a pivot by a string or a very light rod so that it can swing freely. When displaced to an initial angle and released, the pendulum will swing back and forth with a periodic motion. By applying Newton’s second law of motion for rotational systems, the equation of motion for the pendulum may be obtained.

Although the pendulum has a long history, Italian scientist Galileo Galilei was the first to study the properties of pendulums, beginning around 1602.

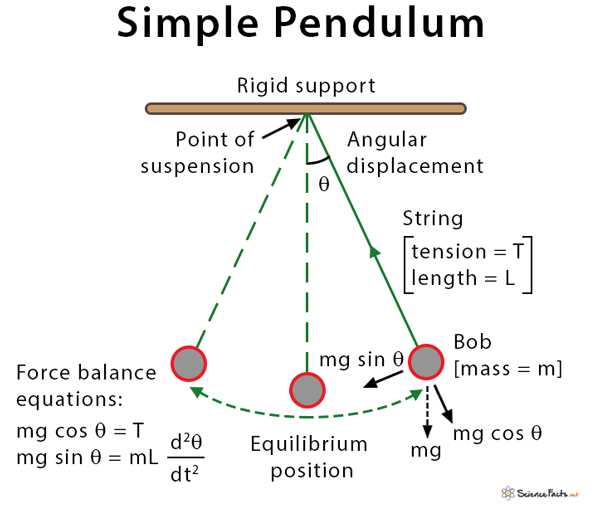
Length (L): Distance between the point of suspension to the center of the bob

Time Period (T): Time taken by the pendulum to finish one full oscillation

Linear Displacement (x): Distance traveled by the pendulum bob from the equilibrium position to one side.

Angular Displacement (θ): The angle described by the pendulum with an imaginary axis at the equilibrium position is called the angular displacement.

Amplitude (x_max): Maximum distance traveled by the pendulum from the equilibrium position to one side before changing its direction. For angle, it is denoted by θ_max.

How to Derive the Formula for Time Period

According to Newton’s second law,

F = ma

The equation can be written in differential form as

If the amplitude of displacement is small, then the small-angle approximation holds, i.e., sin θ ~ θ.

This equation represents a simple harmonic motion. Thus, the motion of a simple pendulum is a simple harmonic motion with an angular frequency, \( \omega = \sqrt{\frac{g}{L}} \), and linear frequency, \( f = \frac{1}{2\pi}\sqrt{\frac{g}{L}} \). The time period is given by,

Performing dimension analysis on the right side of the above equation gives the unit of time.

[L/LT^-2]^1/2 = [T]

The principle of a simple pendulum can be understood as follows. The restoring force of the pendulum from the above is, F = -mgL θ. This force is responsible for restoring the pendulum to its equilibrium position. However, due to the inertia of motion, the pendulum passes the equilibrium position and swings to the other side. This motion is periodic and can be solved using differential equation analysis.

After solving the differential equation, the angular displacement is given by

θ = θ_max sin (ωt)

Sometimes, a phase φ is added to the above equation depending upon the initial conditions of the pendulum. Then, the equation can be written as

θ = θ_max sin (ωt + φ)

A simple pendulum is a typical laboratory experiment in many academic curricula. Students are often asked to evaluate the value of the acceleration due to gravity, g, using the equation for the time period of a pendulum. Rearranging the time period equation,

Note that the component mg cos θ is balanced by the tension T of the string, i.e., T = mg cos θ.

1. Law of mass: The time period is independent of the mass of the bob.
2. Law of length: The time period is directly proportional to the square root of the length.
3. Law of Iscochronism: The time period is independent of the amplitude as long as the amplitude is small.
4. Law of gravity: The time period is inversely proportional to the square root of the acceleration due to gravity at that place.

• Pendulum clock – A common household item. Every time the pendulum swings, the clock’s hand advances at a fixed rate, thus giving the time.
• Old seismometers – A pendulum with a stylus at its bottom was connected to a frame. During an earthquake, the frame moves and causes the stylus to form a pattern on paper.
• Pendulum gravimeter – A pendulum is used to measure the local gravity.
• Foucault’s pendulum – A device to measure the rotation of the earth.
• Metronome – A device used by musicians. It emits a click or a light for each beat of a predetermined interval.