Rotational Kinetic Energy

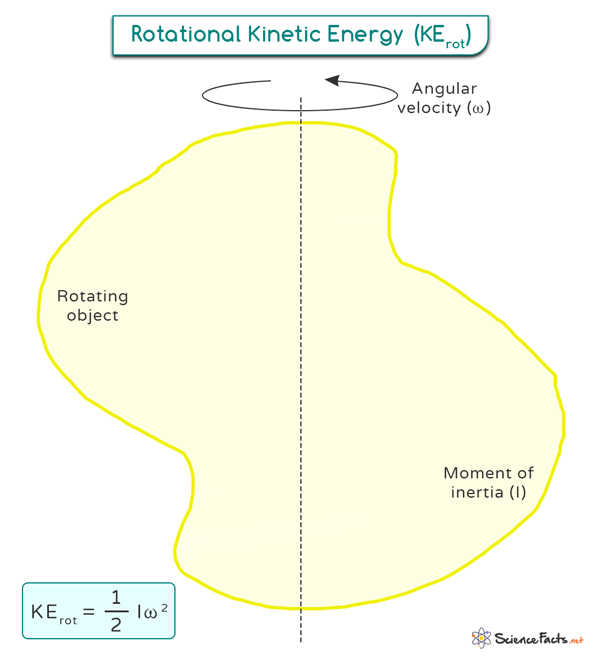
Rotational kinetic energy depends on:

• How fast the object is spinning
• How much mass the spinning object has
• Where the mass is located compared to the spin

The formula for rotational kinetic energy is given by:

KE_rot = ½ Iω²

where 

KE_rot is the rotational kinetic energy

I is the moment of inertia 

ω is the angular velocity

This formula shows that the rotational kinetic energy is directly proportional to the square of the angular velocity and the object’s moment of inertia. Angular velocity represents how quickly an object is rotating. The moment of inertia depends on both the mass and distribution of mass within the object. Objects with more mass concentrated farther from the axis of rotation have higher moments of inertia, resulting in higher rotational kinetic energy for a given angular velocity. 

Unit and Dimension

The SI unit of rotational kinetic energy is Joule (J), which is equivalent to kg m²/s². This unit is derived from the formula for rotational kinetic energy, where the moment of inertia is expressed in kg m² and angular velocity in rad/s. It is important to note that this unit aligns with the fundamental principles of energy and motion in the metric system. The dimensional formula is [M¹L²T^-2]. 

Here are a few examples of rotational kinetic energy:

1. Rolling Solid Sphere

Imagine a solid sphere rolling down a hill. As the sphere descends, it possesses both translational and rotational motion. The sphere’s rotation around its axis contributes to its rotational kinetic energy. The translational and rotational kinetic energies determine the sphere’s overall energy as it moves downhill.

2. Rotating Cylinder

Visualize a cylindrical object, like a can, spinning around a fixed axis. The rotation of the cylinder gives rise to its rotational kinetic energy. The moment of inertia of the cylinder plays a significant role in determining how much energy is stored in its rotation. The greater the moment of inertia and the faster the cylinder spins, the more rotational kinetic energy it possesses. This principle applies to a wide range of rotating objects, from wheels to cylinders used in machinery.

3. Spinning Top

A spinning top is a classic example of an object exhibiting rotational kinetic energy. As the top spins around its central axis, it possesses energy due to its angular velocity and moment of inertia. The top’s ability to remain upright while spinning results from the conservation of angular momentum, a concept closely related to rotational dynamics. The interplay between its motion and the stored rotational energy enables the top to exhibit its fascinating spinning behavior.

4. Rotating Wind Turbine 

The rotating blades of a wind turbine exemplify the conversion of wind energy into rotational kinetic energy. As the wind pushes against the blades, they rotate around their axis. This rotational motion is then transformed into electrical energy through generators. The design of wind turbines takes into account factors such as blade shape, size, and wind speed to optimize the extraction of rotational kinetic energy from the wind.

5. Planet 

On a cosmic scale, the rotation of planets is governed by rotational kinetic energy. Planets like Earth rotate on their axes, alternating between day and night. The rotation of a planet involves a massive amount of energy due to its substantial moment of inertia and relatively slow rotation rate. This rotational kinetic energy contributes to phenomena like the Coriolis effect, which influences atmospheric and oceanic currents and shapes planetary features over geological timescales.

Rotational kinetic energy is a fundamental concept in physics crucial in various applications. Understanding the applications of rotational kinetic energy can help us comprehend and analyze the behavior of rotating objects and systems.

1. One prominent application of rotational kinetic energy is found in the field of mechanical engineering. Rotating machinery, such as turbines, engines, and motors, rely on rotational kinetic energy to convert mechanical power into useful work. By harnessing the rotational motion of these machines, we can generate electricity, propel vehicles, or drive industrial processes. Calculating and optimizing rotational kinetic energy allows engineers to design more efficient and reliable systems.
2. Another area where the concept of rotational kinetic energy finds practical use is in sports and athletics. Activities like discus throwing, shot put, hammer throw, or even gymnastics involve spinning or rotating movements. Understanding how rotational kinetic energy relates to angular velocity and moment of inertia helps athletes maximize their performance by optimizing their technique and generating more power during their movements.
3. Rotational kinetic energy also plays a significant role in understanding celestial bodies’ dynamics. Planets, moons, asteroids, and other astronomical objects exhibit rotation as they orbit around their axis or revolve around larger bodies like stars. Astronomers can better understand phenomena such as planetary formation processes or celestial mechanics by studying the principles governing rotational motion principles and calculating the associated kinetic energies involved.

Problem 1: Calculate the rotational kinetic energy of a flywheel whose moment of inertia is 0.1 kg m² and angular velocity is 5 rad/s.

Solution

Given I = 0.1 kg m² and ω = 5 rad/s

The rotational kinetic energy is:

KE_rot = ½ × 0.1 × (5)² = 1.25 J

Problem 2: Determine the rotational kinetic energy of a planet rotating at 1 × 10^-4 rad/s with a moment of inertia of 8 × 10³⁴ kg m².

Solution

Given I = 8 × 10³⁴ kg m² and ω = 1 × 10^-4 rad/s

The rotational kinetic energy is:

KE_rot = ½ × 8 × 10³⁴ × (1 × 10^-4)² = 4 × 10^-25 J

Problem 3: Suppose a solid sphere with a mass of 2 kg and a radius of 0.5 m rotates at an angular velocity of 4 rad/s. What is its rotational kinetic energy?

Solution

Given M = 2 kg, R = 0.5 m, and ω = 4 rad/s

The moment of inertia of a solid sphere is (2/5)MR².

I = (2/5)MR² = (2/5) × 2 × (0.5)² = 0.2 kg m²

The rotational kinetic energy is:

KE_rot = (1/2) × 0.2 × (4)² = 1.6 J

Problem 4: Suppose we have a solid cylinder with a mass of 4 kg and a radius of 0.3 m, rotating at an angular velocity of 6 rad/s. What is its rotational kinetic energy?

Solution

Given M = 4 kg, R = 0.3 m, and ω = 6 rad/s

The moment of inertia of a solid cylinder is (1/2)MR².

I = (1/2)MR² = (1/2) × 4 × (0.3)² = 0.18 kg m²

The rotational kinetic energy is:

KE_rot = (1/2) × 0.18 × (6)² = 1.6 J

= 3.24 J