Rotational Motion

• Earth rotating about its axis
• Subatomic particles rotating in a cyclotron
• A skater exhibiting rotation during her routine
• A wheel rolling down a hill
• A football spinning in its trajectory
• A phonograph’s turntable rotating about a pin
• A potter’s wheel rotating about its center

The following are examples of rotational motion, although they may not seem so. The reason is that the angle through which the objects rotate is slight and does not complete a full circle.

• Children playing on a see-saw
• Opening a door
• Turning a wrench
• A pendulum swinging about its pivot point

Angle of Rotation

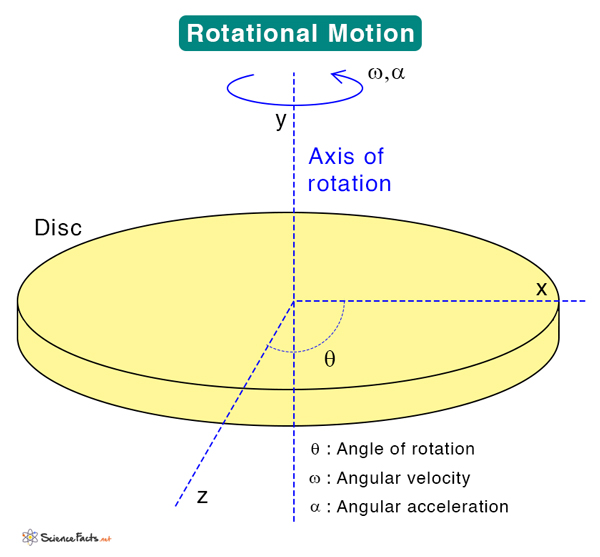
An object rotating about an axis is defined by its angle of rotation, θ. Its analogy is similar to distance in linear motion. It tells us how much the object has spun. It is a time-dependent variable that is convenient to measure. Its unit is degree or radian. When the object completes one rotation, the angle it describes is 360˚ or 2π radian.

Angular Velocity

The angular velocity, ω, is defined as the rate at which the object spins. It is analogous to linear velocity. It is given by the change in the angle of rotation divided by the change in time.

It has a unit of radians per second or rad/s.

Angular Acceleration

The rate at which the angular velocity changes is called angular acceleration, similar to acceleration in linear motion. It is denoted by the symbol α and, mathematically, given by

It has a unit of radians per second squared or rads/s².

The sign of α depends on whether ω increases or decreases with time. If ω is increasing with time, then α is positive. If ω is decreasing with time, then α is negative.

Let us examine how the quantities θ, ω, and α are related. Using rotational kinematics, the relationship among these physical entities is given by

Where ω_o is known as the initial angular velocity. It is the velocity of the rotating object at time t = 0.

Torque

Torque is the angular version of force. It is the turning efficiency of the force. For example, we apply torque to operate a merry-go-round. Force is generally applied on the lever arm to rotate an object about its axis. Mathematically, torque is given by the following equation:

Where,

τ: Torque

F: Force applied

r: Distance of the applied force from the rotation axis or the length of the lever arm

θ: Angle of rotation

The unit of force is Newton or N, and the unit of distance is meter or m. Therefore, the unit of torque is Newton·meter or N·m.

Newton’s second law for rotational motion states that every object will move with a constant angular velocity unless acted upon by a torque.

Tangential Velocity and Tangential Acceleration

A rotating object also has a tangential velocity and a tangential acceleration. Tangential velocity is the instantaneous linear velocity of the object. The relationship between tangential velocity v and angular velocity ω is given as follows:

This equation says that the tangential speed v is proportional to the distance r from the center of rotation. Consider an object rotating about its axis that passes through the center, like a CD. A point closer to the center will have a lower tangential velocity than a distant point. The distant point makes a longer arc length simultaneously with the closest point. Both these points will have the same angular velocity.

The rate of change of tangential velocity gives the tangential acceleration a. The relationship between tangential acceleration and angular acceleration is as follows:

The magnitudes of tangential acceleration and angular acceleration are directly proportional to each other. The higher the angular acceleration, the greater the tangential acceleration, provided the object’s radius remains constant.

Problem 1. How much torque does a person produce if he applies an 8 N force 2 m away from the rotation axis, perpendicularly to the lever arm?

Solution

Given

F = 8 N

r = 2 m

θ = 0˚

The torque is given by

τ = r F cos θ

or, τ = 2 m * 8 N * cos 0

or, τ = 16 N·m

Problem 2. An object’s angular velocity changes from 5 rad/s clockwise to 10 rad/s clockwise in 4 s. What is its angular acceleration?

Solution

Given

ω₁ = 5 rad/s

ω₂ = 10 rad/s

t = 4 s

The angular acceleration is given by

α = (ω₂ – ω₁)/t

or, α = (10 rad/s – 5 rad/s)/4s

or, α = 1.25 rad/s