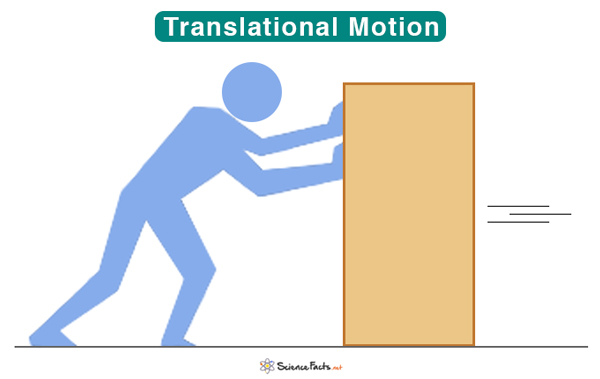
Home / Physics / Translational Motion

Translational Motion

Translation motion, also known as translatory motion, occurs when all points of a rigid body move tandemly. There is no change in the object’s orientation relative to a fixed point—only the object shifts from one position to another. All points on the object have the same velocity and acceleration in magnitude at every instant. In other words, all points have the same trajectory. Translational motion can occur in one, two, or three dimensions.

Types of Translational Motion

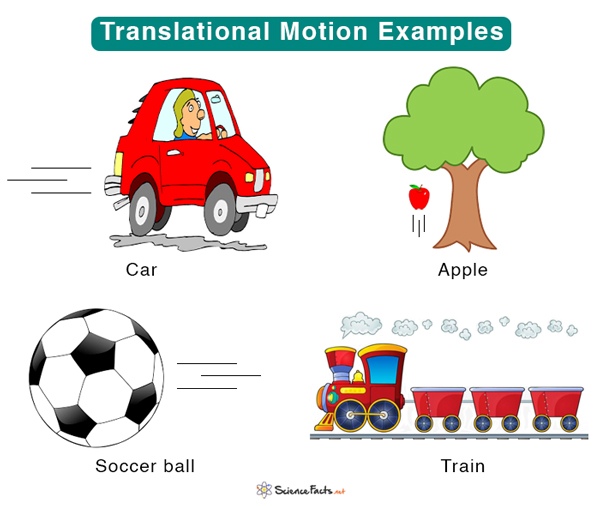
1. Rectilinear Motion

In a rectilinear motion, the object moves in a straight line in a well-defined path. It is a one-dimensional motion.

Examples

A train moving on its track
A man walking down a path
Birds flying in the sky
A boat sailing down a river

2. Curvilinear motion

In a curvilinear motion, the motion of an object is in a curve path whose trajectory follows the laws of motion. It can occur in two or three dimensions.

A projectile passing through the air
A bullet fired from a gun
A racing car around a bend
A stone undergoing a slingshot

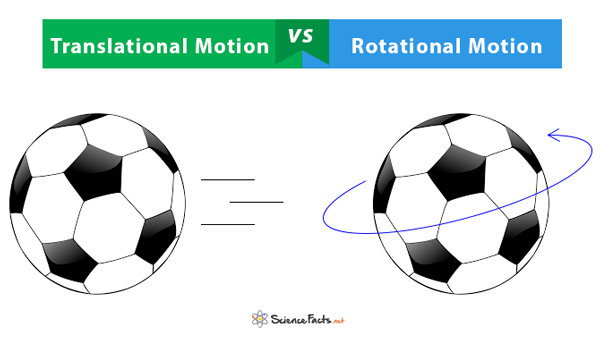
Difference Between Translational and Rotational Motion

Translational motion involves the movement of an object in one or more dimensions. On the other hand, rotational motion involves the continuous spinning of an object about an imaginary axis. There is a strong analogy between the two.

The table below compares the physical quantities associated with translational and rotational motions.

Translational Motion: Physical Quantity	Translational Motion: Symbol and Equation	Rotational Motion: Physical Quantity	Rotational Motion: Symbol and Equation
Displacement	x	Angle	θ
Linear Velocity	v = dx/dt	Angular Velocity	ω = dθ/dt
Linear Acceleration	a = dv/dt	Angular Acceleration	α = dω/dt
Mass	m	Moment of inertia	I
Force	F = ma	Torque	τ = Iα
Work	W = Σ F Δx	Work	W = Σ τ Δθ
Power	P = Fv	Power	P = τω
Kinetic Energy	K.E. = ½ m v²	Kinetic Energy	K.E. = ½ I ω²

References
- 1. What is translational motion? – Physicscatalyst.com
  2. Translational and Rotational Motion – G9toengineering.com
  3. Translational Motion vs. and Rotational Motion Farside.ph.utexas.edu
  4. Difference Between Translational and Rotational Motion –Study.com