Centripetal Force
What is Centripetal Force
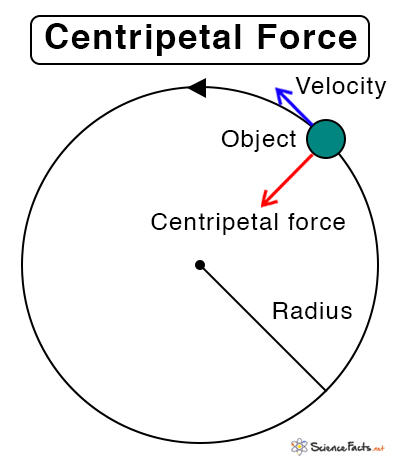
Centripetal force is responsible for keeping an object moving in a curved path. It is caused by an object’s motion around a curve or circular path.
What is the Direction of the Centripetal Force
The centripetal force is directed towards the center of curvature of the curved path traced by the object. It is at a right angle to the object’s motion and causes the object to change its direction.
How Does the Centripetal Force Affect Circular Motion
In a circular motion, the centripetal force is along the radius toward the center.
Examples and Applications of Centripetal Force
Here are some examples, applications, and uses of the centripetal force in everyday life.
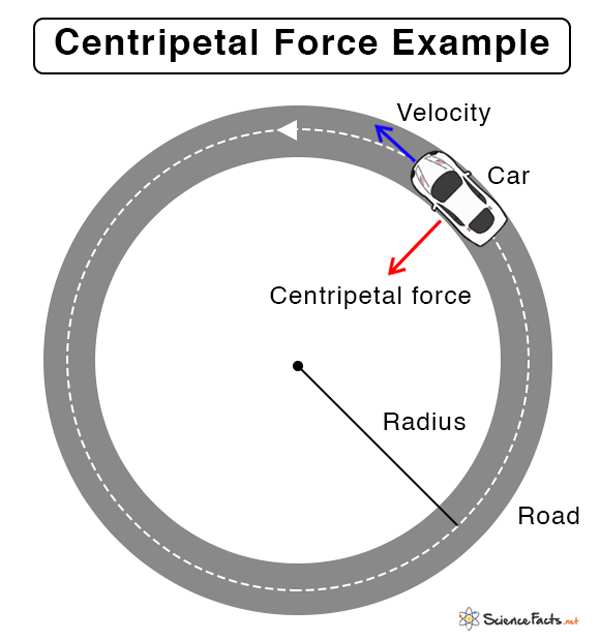
- The force experienced by a car when it makes a turn on a circular road, as shown below
- The Earth’s gravitational force keeps satellites in orbit and causes centripetal motion
- The Earth’s gravity is responsible for keeping objects on the surface
- The tension force on a string swirling a bucket of water
- The force experienced by a roller coaster in an amusement park when going around a loop
- The force experienced by a pendulum while swinging
Centripetal Force Equation
The centripetal force can be measured by using the concept of mass and inertia. Newton’s laws of motion describe the movement of all objects having mass. Hence, Isaac Newton is considered to discover centrifugal force. The centripetal force can be found using Newton’s second law. According to this law, the force F on an object is given by the mass m times acceleration a.
F = ma
Linear and Angular Velocity
The angular velocity of an object in a circular motion is defined as the rate at which it turns around its path. Suppose the object describes an angle θ in time t, then the angular velocity ω is given by
ω = θ/t
The relationship between the angular velocity ω and linear velocity v is given by
v = ωr
Here, r is the radius of the circular path.
Centripetal Acceleration
An object moving in a circular path experiences acceleration known as centripetal acceleration. This acceleration is directed radially inward and is given by
a = ω2r = v2/r
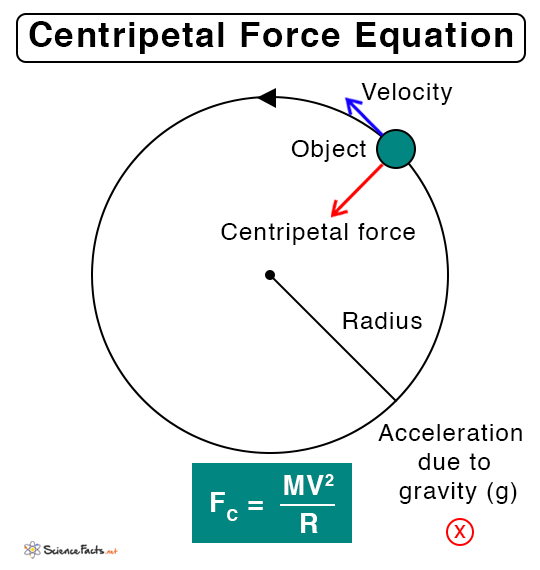
Therefore, the magnitude of the centripetal force is given by
FC = mv2/r
Unit: Newton or N
Dimension: MLT-2
Work Done by Centripetal Force
The object moves in a circle of constant radius. The centripetal force is always directed toward the center. In this case, the force and the displacement vectors are at right angles. Therefore, the work done by the centripetal force is zero.
Difference Between Centripetal and Centrifugal Force
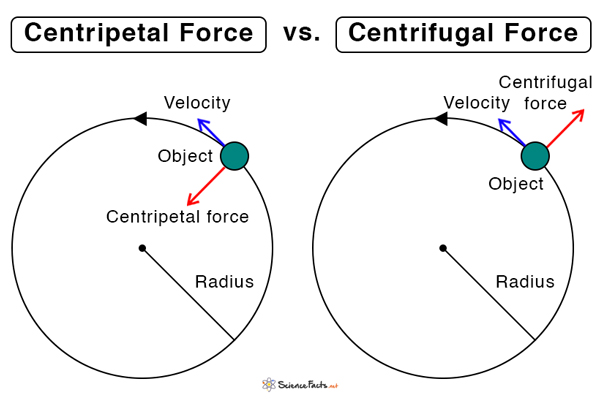
There are some differences between the centripetal and the centrifugal force. The centripetal force is directed towards the center of curvature of the curved path. In contrast, the centrifugal force is directed away from the center. The centripetal force is real to an observer in an inertial frame of reference, whereas the centrifugal force is virtual. Also known as pseudo force, the centrifugal force is observed by an observer in the non-inertial frame, i.e., the stationary frame.
Centripetal Force vs. Centrifugal Force
| Centripetal Force | Centrifugal Force | |
| Type of force in an inertial frame | Real. Observed. | Virtual. Not observed. |
| Direction | Inward. Directed towards the center. | Outward. Directed away from the center. |
| Example | The force that pulls a car inward. | The outward force that the passengers feel in a car. |
Example Problems
P.1. Calculate the centripetal force exerted on a 1200 kg car that goes around a 600 m radius curve at 20.0 m/s.
Soln.: Given,
m = 1200 kg
r = 600 m
v = 20 m/s
FC = mv2/r = 1200 kg x (20 ms-1)2 / 600 m = 800 N
P.2. An object of mass 20 kg is in a circular orbit of radius 20 m at a velocity of 20 m/s. Calculate the centripetal force required to maintain this orbit.
Soln.: Given,
m = 20 kg
r = 20 m
v = 20 m/s
FC = mv2/r = 20 kg x (20 ms-1)2 / 20 m = 400 N
-
References
Article was last reviewed on Tuesday, August 1, 2023








Good pictures. Completely correct. Amond the many resources that get it right, see https://www.sciencefacts.net/centripetal-force.html . *
In order to continue turning, an inward pointing centripetal force (static friction between tires and road in this case) is necessary. That force produces an inward centripetal acceleration which changes the direction of the velocity, hence the car turns.
* Even this resource makes a mistake, saying about the centrifugal force, “The outward force that the passengers feel in a car.” No, they don’t. Instead they feel an inward force of the seat belts and the doors which luckily keep them in the car.
In other words, there is no example for centrifugal force – it doesn’t exist.
Andy Veh, University of Alaska Physics Professor