Oscillatory Motion

Here are some examples of oscillatory motion.

• Oscillations of a pendulum
• Vibration in a spring
• Motion of a wheel
• Movement of a seesaw
• Vibrations in guitar strings
• Alternating current in household equipment
• Electromagnetic waves passing through the air

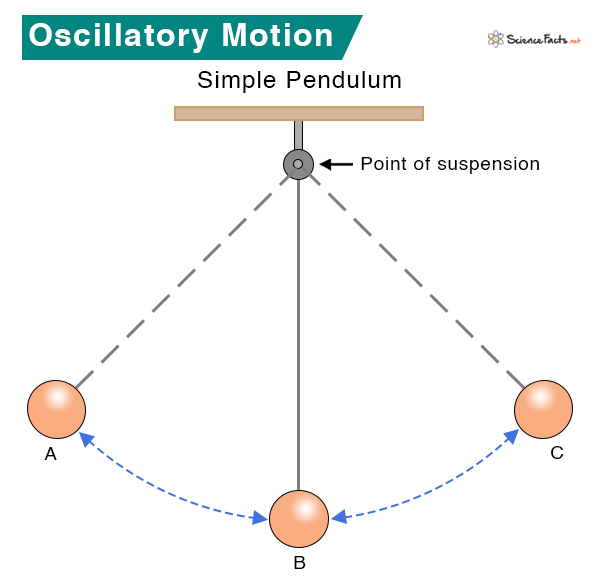
The example below shows a pendulum oscillating about its point of suspension. It passes through points A, B, and C during its oscillations.

A simple harmonic motion is an oscillatory motion in which an object moves to and fro along a straight line about an equilibrium position. Its vibrations are said to be linear. The object’s motion is such that the restoring force changes its direction and tends to bring it back to the equilibrium position. However, due to the stiffness and inertia of the object, it shoots past the equilibrium position. The process repeats and results in an oscillatory motion. The object’s kinetic and potential energy changes over time. The sum of the two remains constant due to the energy conservation law.

Equation

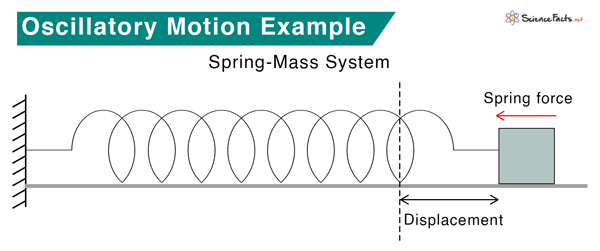
Consider a spring-mass system on a horizontal surface, as shown in the image. According to Hooke’s law, the restoring force on the oscillating object is proportional to its displacement.

Where

F is the restoring force

x is the displacement

k is the spring constant

From Newton’s second law

Where

m is the mass of the object

\(\frac{d^2 x}{dt^2} \) is the acceleration expressed in differential form

Comparing the two equations

Where \( \omega = \sqrt{\frac{k}{m}} \)

The above equation is a second-order linear differential equation whose solution is given by

Where

A is the amplitude

ω is the angular frequency

t is the time

ø is the phase difference

The constants A, ω, and ø can be determined by the boundary conditions of the system.

In the discussion above, we have neglected the frictional force in the system. Generally, friction occurs between the object and the horizontal surface on which it oscillates. The result is that the oscillations tend to decay with time. Such oscillatory motion, where a damping or resistive force is present, is called damped harmonic motion.

Equation

Consider the spring-mass system again, but it acts like a damped oscillator this time. The damping force is found to be proportional to the object’s velocity. The second-order differential equation modifies to

Where b is an arbitrary constant. The term \( b \frac{dx}{dt} \) is the damping force. Rewriting the equation as

Where \( 2\beta = \frac{b}{m} \) and \( \omega_o = \sqrt{\frac{k}{m}} \) The general solution of this equation is

Where \( \omega_1 = \sqrt{\beta^2 – \omega_{o}^2} \)

The exponential term in the expression is the decay function, and β is the damping coefficient. There are three types of damped oscillators:

• under-damped, when β < ω_o
• over-damped, when β > ω_o
• critically damped, when β = ω_o